本文系统解析二维与三维图形变换的核心原理，涵盖模型、视图、投影变换及齐次坐标系的应用。深入讲解缩放、旋转、平移、正交与透视投影的实现，结合Rodrigue公式与组合变换策略，助力理解计算机图形学中的空间转换与渲染逻辑。（Generated by DeepSeek r1）

Transformation

为什么要用变换

Modeling 模型变换

模型通过各种变换可以按某种方式自然地改变形状

Viewing 视图变换

三维世界到二维世界投影的过程中涉及大量的视图变换

二维线性变换的类型

缩放 Scale

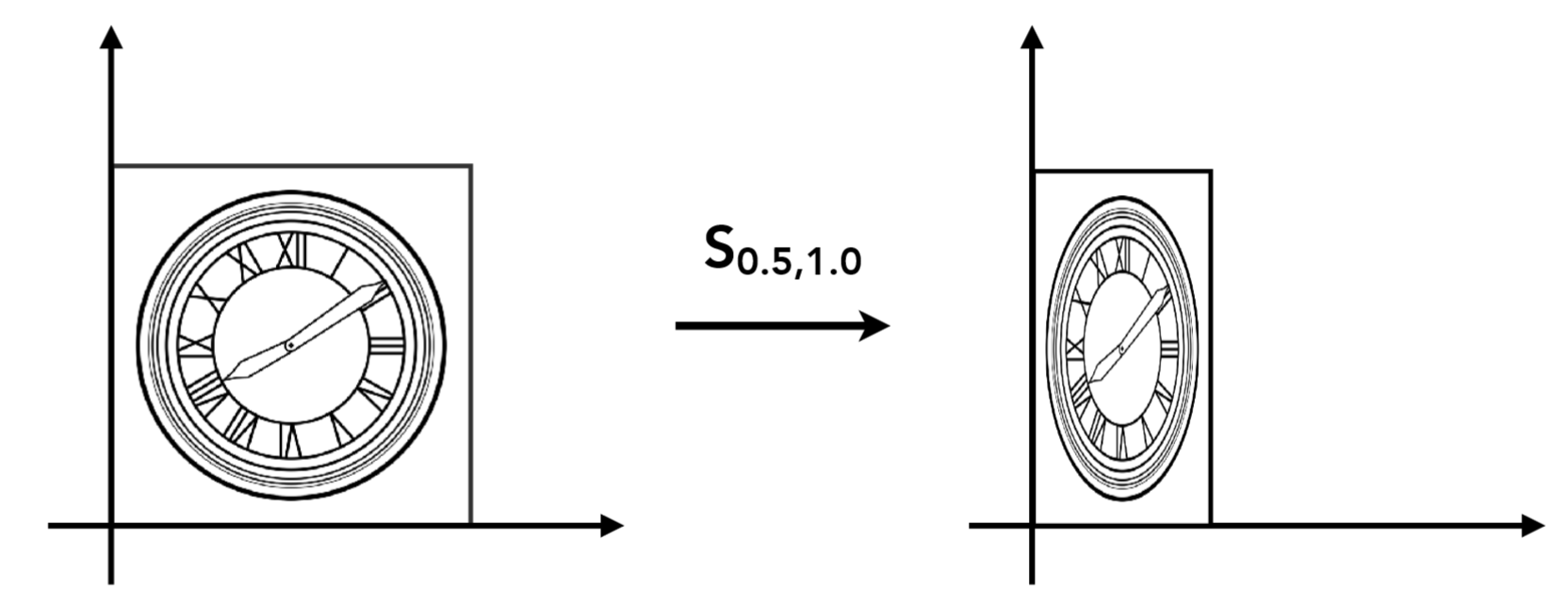
$$
\begin{bmatrix}
x^\prime \
y^\prime
\end{bmatrix} =
\begin{bmatrix}
s_x & 0 \
0 & s_y
\end{bmatrix}
\begin{bmatrix}
x \
y
\end{bmatrix}
$$

反转 Reflection

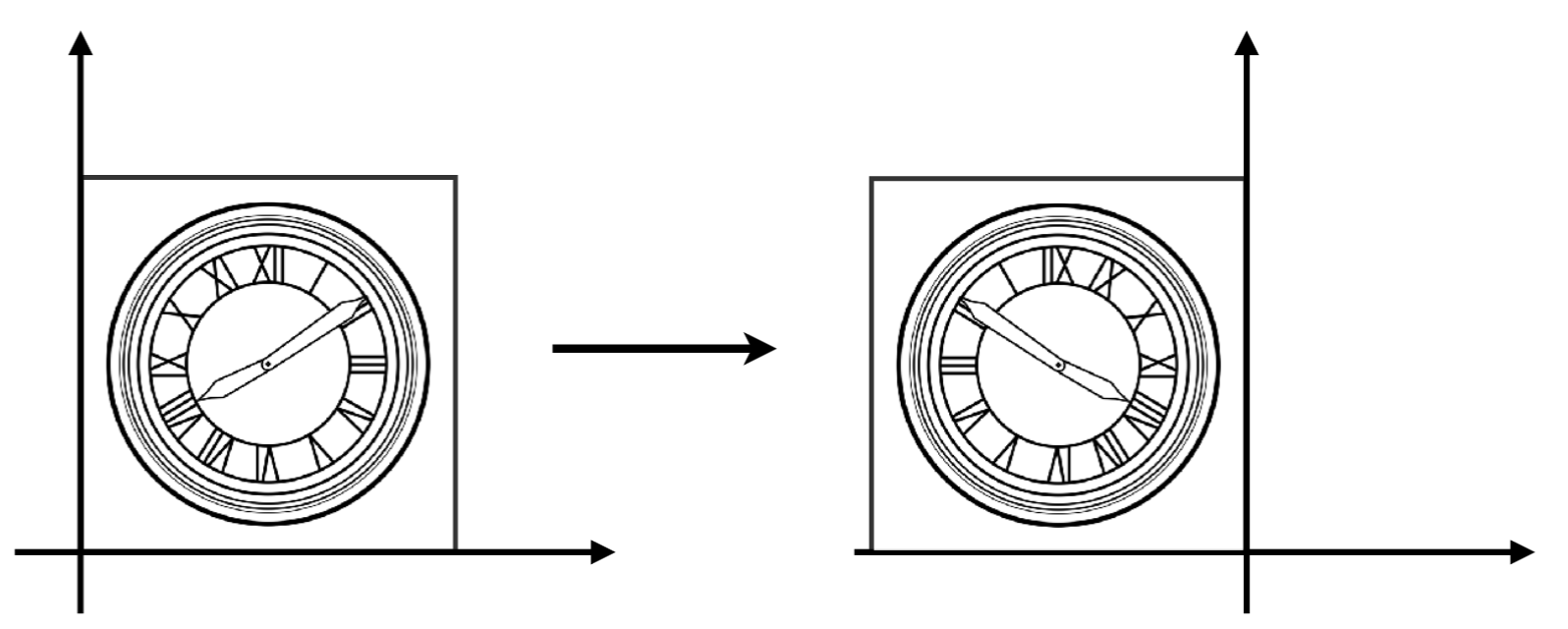
$$
\begin{bmatrix}
x^\prime \
y^\prime
\end{bmatrix} =
\begin{bmatrix}
-1 & 0 \
0 & 1
\end{bmatrix}
\begin{bmatrix}
x \
y
\end{bmatrix}
$$

切变 Shear

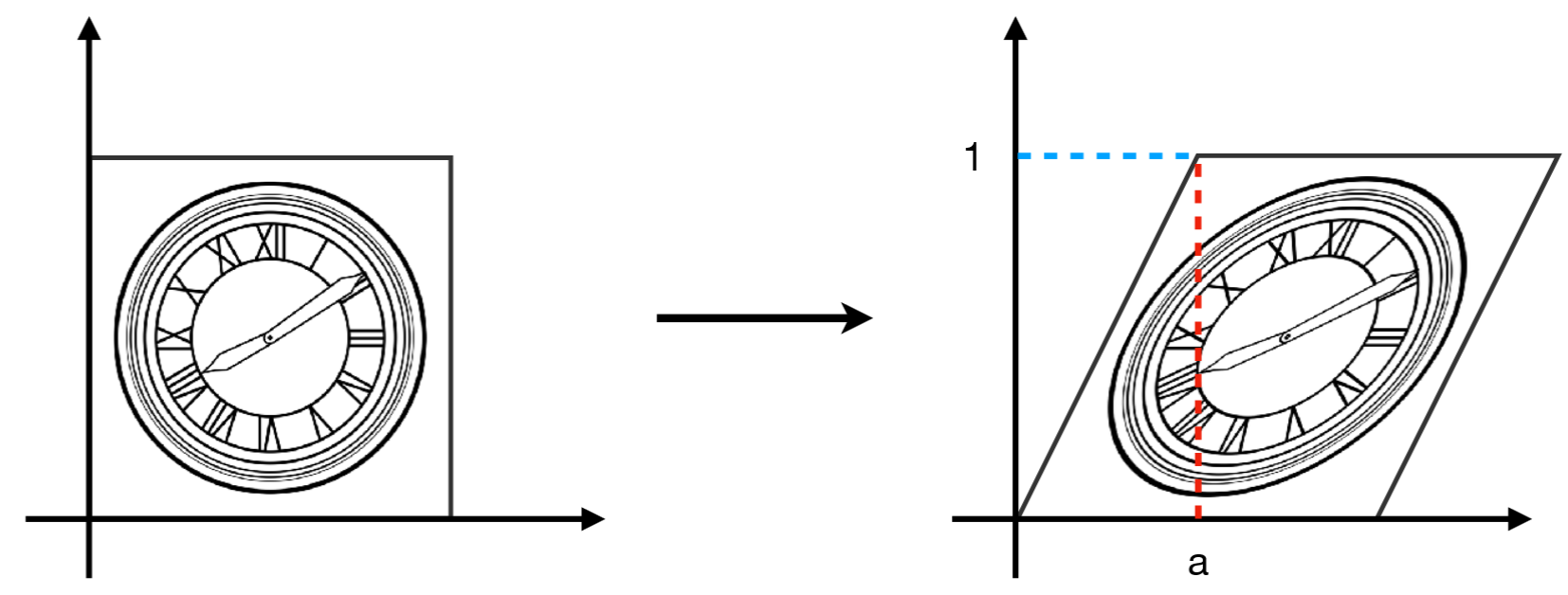
分析可知，在 $y = y_0$ 的高度上，$y$ 的变化量为 $0$，$x$ 的变化量为 $ay$。
$$
\begin{bmatrix}
x^\prime \
y^\prime
\end{bmatrix} =
\begin{bmatrix}
1 & a \
0 & 1
\end{bmatrix}
\begin{bmatrix}
x \
y
\end{bmatrix}
$$

旋转 Rotate

默认：绕 $(0, 0)$、逆时针方向旋转

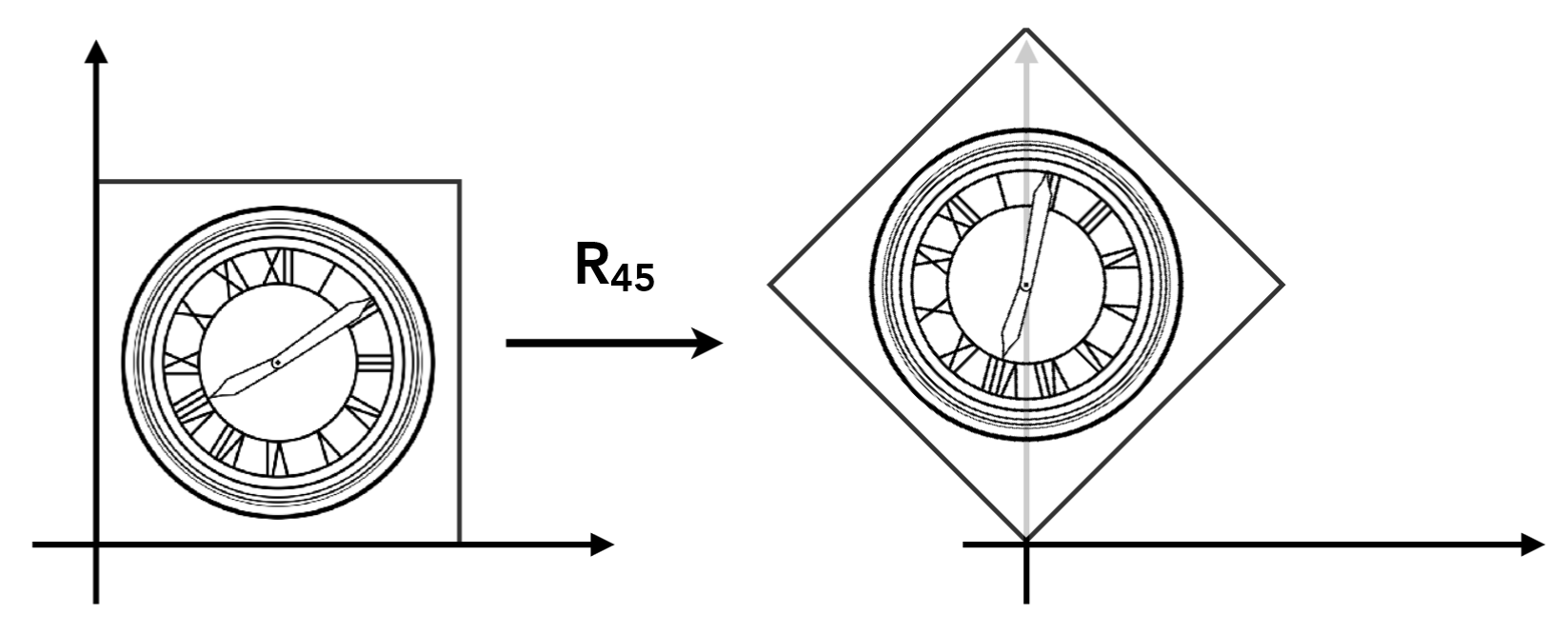
考虑 $\hat i$ 和 $\hat j$ 变换之后的位置，可得：
$$
\begin{bmatrix}
x^\prime \
y^\prime
\end{bmatrix} =
\begin{bmatrix}
\cos \theta & -\sin \theta \
\sin \theta & \cos \theta
\end{bmatrix}
\begin{bmatrix}
x \
y
\end{bmatrix}
$$
可以记系数矩阵为 $R_\theta$。

特性：旋转的逆等于旋转的转置 $R_\theta^{-1} = R_\theta^T$，所以它是正交矩阵。

齐次坐标系

为什么要引入

考虑平移变换：
$$
x^\prime = x + t_x\
y^\prime = y + t_y
$$
发现并不能用前面的矩阵乘法来描述此变换，因为平移并不是线性变换。

线性变换 $+$ 平移变换 $=$ 仿射变换：
$$
\begin{bmatrix}
x^\prime \
y^\prime
\end{bmatrix} =
\begin{bmatrix}
a & b \
c & d
\end{bmatrix}
\begin{bmatrix}
x \
y
\end{bmatrix} +
\begin{bmatrix}
t_x \
t_y
\end{bmatrix}
$$
统一化的解决方法：使用齐次坐标系。

表示方法

对于每个二维点，再加一维 $1$；对于每个二维向量，再加一维 $0$。
$$
\begin{bmatrix}
x^\prime \
y^\prime \
w^\prime
\end{bmatrix} =
\begin{bmatrix}
1 & 0 & t_x \
0 & 1 & t_y \
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x \
y \
1
\end{bmatrix} =
\begin{bmatrix}
x + t_x \
y + t_y \
1
\end{bmatrix}
$$
如果一个矩阵的 $w$ 不为 $0$ 或 $1$，则不是一个合法的齐次坐标表示。
$$
\begin{bmatrix}
x \
y \
w
\end{bmatrix} =
\begin{bmatrix}
x / w \
y / w \
1
\end{bmatrix} (w \neq 0)
$$
多个点的齐次坐标相加的结果：各点的重心。

在仿射变换中：齐次坐标的左上角 $2 \times 2$ 子矩阵负责线性变换；前两行的第 3 位用于平移；第三行固定为 $[0, 0, 1]$。

组合变换

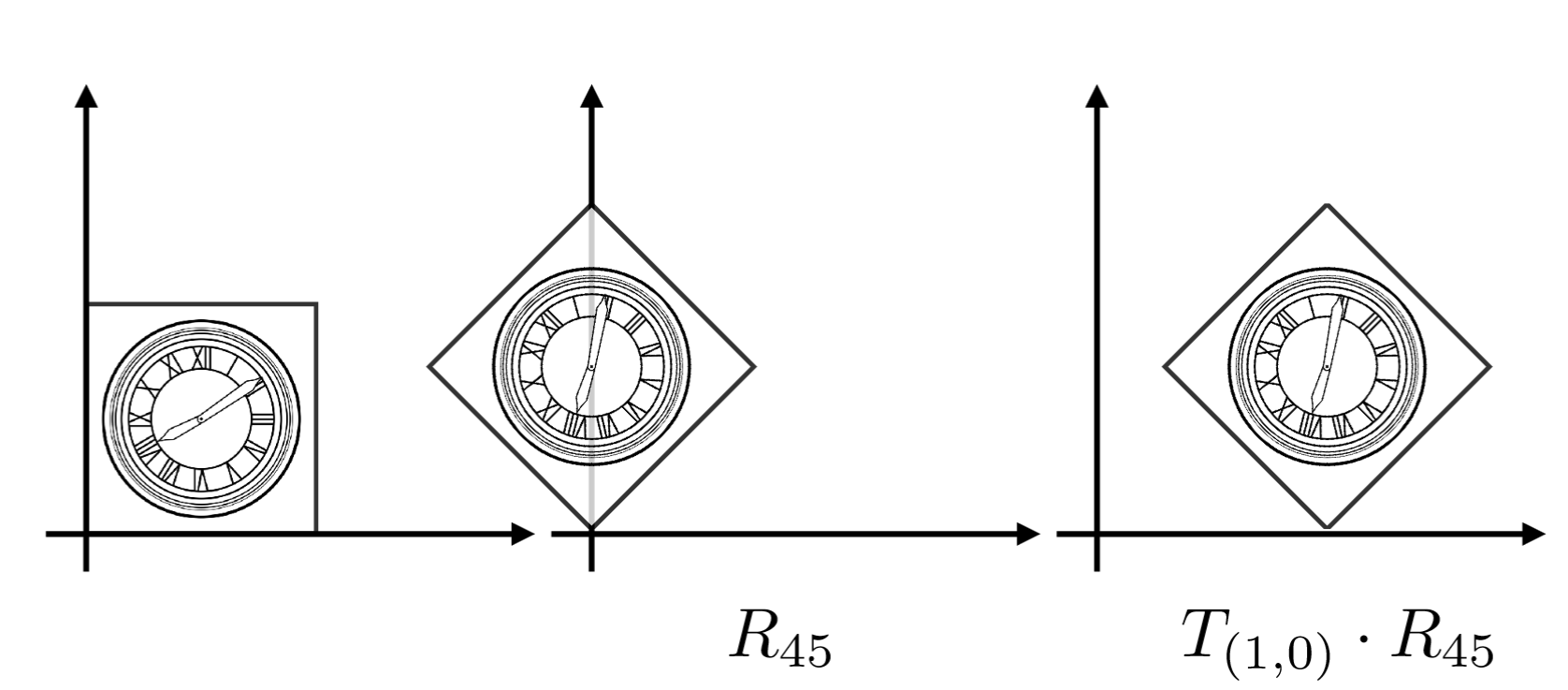
各个基础变换的组合：矩阵左乘，先应用的变换对应的矩阵在右边

$$
A_n(\cdots A_2(A_1(x))) = A_n \cdots A_2 \cdot A_1 \cdot
\begin{bmatrix}
x \
y \
1
\end{bmatrix}
$$

三维变换

三维齐次坐标可以由二维推出：
$$
\begin{bmatrix}
x^\prime \
y^\prime \
z^\prime \
1
\end{bmatrix} =
\begin{bmatrix}
a & b & c & t_x \
d & e & f & t_y \
g & h & i & t_z \
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x \
y \
z \
1
\end{bmatrix}
$$
左上角的 $3 \times 3$ 矩阵完成线性变换，注意是先应用线性变换再应用平移。