GAMES101: Ray Tracing
|
9
|
0
|
课程笔记

4574 字
|
29 分钟

本文系统讲解现代光线追踪技术的核心原理与实现，从基础的Whitted风格光线追踪到基于蒙特卡洛积分的路径追踪方法，全面解析辐射度量学中的Radiance、Irradiance等关键概念，详细介绍渲染方程的数学表达，同时深入探讨全局光照的实现原理。(Generated by DeepSeek r1)

光线追踪

为什么使用光线追踪

光栅化存在问题：

  • 不好表示全局效果
    • 阴影（shadow mapping），只能做硬阴影
    • Glossy Reflection（像镜子但又不完全一样的反射材质称为 Glossy）
    • Indirect Illumination 间接光照，光线弹射超过一次

在性能方面，光栅化速度较快（>30fps）但是质量较低。

光线追踪是一种准确的但很慢的技术（10K CPU 核 * 小时 / 帧）。

基础算法

光线的假设

  1. 光沿直线传播
  2. 光线之间交叉时不会发生碰撞
  3. 光线从光源发出，在场景中反射后进入眼睛（光路的可逆性 reciprocity）

光线投射 Ray Casting

Appel 1968

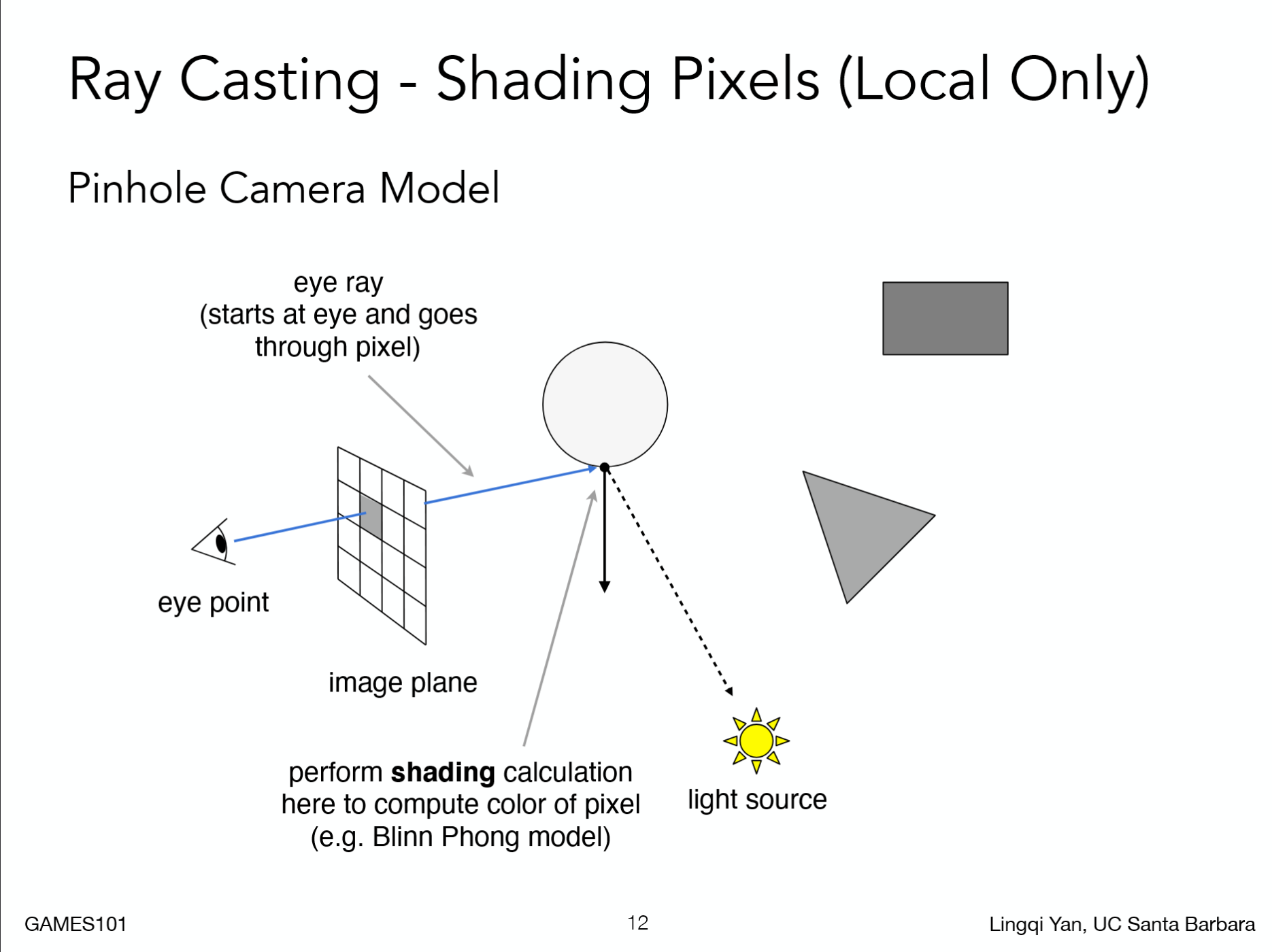
  1. 假设眼睛是针孔摄像机。
  2. 对于画面中的每一个像素，从摄像机发射一条光线（相机光线 eye ray），它可能与物体的某一点相交或者不与任何物体相交。
  3. 对于相交点，发射一条到光源的直线（阴影光线 shadow ray），如果不与任何物体相交，该像素显示物体；如果相交，该像素显示阴影。
  4. 计算着色，显示在画面上。

image-20250626093449225

Whitted Style 光线追踪

上述方法还是只能解决光线只弹射一次的情况，所以需要新的方法。

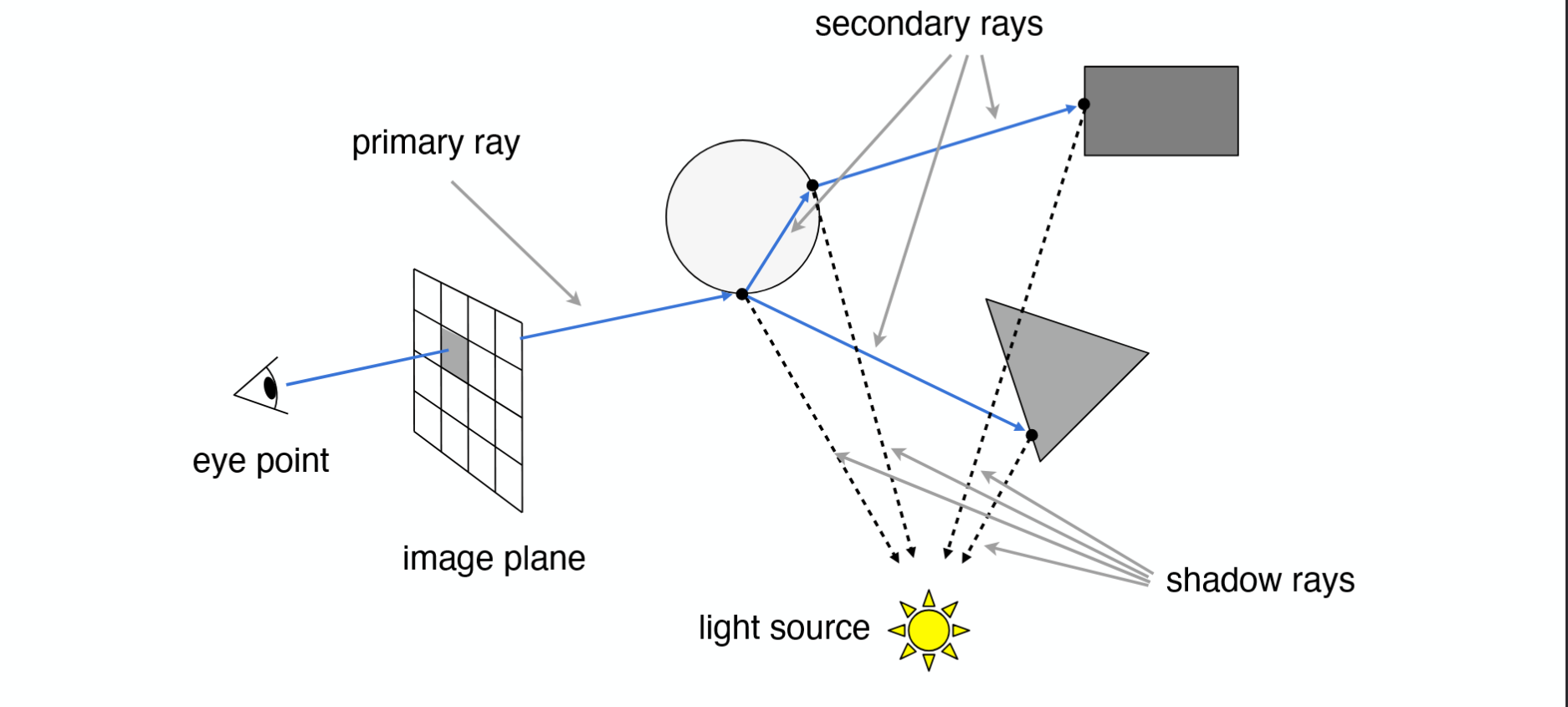
  1. 相机光线打到玻璃材质上，会发生折射和镜面反射。
  2. 显然，折射和反射可以发生多次，所以一条光线会打到多个点上。
  3. 对于每一个接触点，都计算一条阴影光线和着色结果。
  4. 对于没有被遮挡的点，将着色结果都加在画面上。

image-20250626094859249

光线与表面的交点 Ray-Surface Intersection

光线方程

数学上光线就是一条从点光源发出的射线，$\vec r(t) = \vec o + t \vec d, 0 \le t < \infty$。

一般的隐式表面

表面方程 $f(\vec p) = 0$。

带入光线得到 $f(\vec o + t \vec d) = 0$，解出 $t$ 得到 $\vec r(t)$。

球

球的方程：$(\vec p - \vec c)^2 - R^2 = 0$。

交点 $p$ 必须同时满足两个方程，所以有 $(\vec o + t \vec d - \vec c)^2 - R^2 = 0$。

$a t^2 + bt + c = 0$，其中 $a = \vec d^2, b = 2 (\vec o - \vec c)\cdot \vec d,c = (\vec o - \vec c)^2 - R^2$。

求根公式 $t = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$，有意义必须要 $t > 0$。

显式表面

主要是光线和三角形求交，只考虑 0 个或 1 个交点。

简单方法

拆分为两步：

  1. 光线和平面求交
  2. 判断交点是否在三角形内

平面的方程：法线 $\vec n$ + 平面上一个点 $\vec p^\prime$，$(\vec p - \vec p^\prime) \vec n = 0$。

代入得 $(\vec o + t \vec d - \vec p^\prime)\vec n = 0$，$t = \dfrac{(\vec p^\prime - \vec o) \vec n}{\vec d \cdot \vec n}$。

判定 $0 < t < \infty$，再判定是否在三角形内。

Möller Trumbore Algorithm

如果一个点在三角形平面内，那么一定能用重心坐标描述 $\vec o + t \vec d = (1 - b_1 - b_2) \vec p_0 + b_1 \vec p_1 + b_2 \vec p_2$。

解方程得到
$$
\begin{bmatrix}
t\
b_1\
b_2
\end{bmatrix} =
\frac{1}{\vec{S_1} \cdot \vec{E_1}}
\begin{bmatrix}
\vec S_2 \cdot \vec E_2\
\vec S_1 \cdot \vec S\
\vec S_2 \cdot \vec d
\end{bmatrix}
$$
其中 $\vec{E_1} = \vec p_1 - \vec p_0, \vec E_2 = \vec p_2 - \vec p_0, \vec S = \vec o - \vec p, \vec{S_1} = \vec d \times \vec{E_2}, \vec{S_2} = \vec S \times \vec E_1$。总共有 1 个除法，27 个乘法，17 个加法。

通过重心坐标非负判定是否在三角形内。

包围盒 Bounding Volume

对于复杂的物体，先用一个相对简单的形状（包围盒）包围它。如果光线连包围盒都碰不到，那么也碰不到包围盒内的面。

三维使用的基本包围盒：三对平面组成的长方体。

常用的包围和称为轴对齐包围盒 Axis-Aligned Bounding Box。

关键思想：只有光线在所有相对平面内时才认为在包围盒内；离开任意一对相对平面时即离开了包围盒。

二维求交

二维下 AABB 是两对直线组成的长方形。

先计算出光线和每对直线相交的时间（可能有负数），形成两个区间，两个区间的交集就是光线在包围盒内的时间。

使用轴对齐，可以简化 $t$ 的计算：
$$
t = \frac{(\vec p^\prime - \vec o) \cdot \vec n}{\vec d \cdot \vec n} \Rightarrow t = \frac{p^\prime_x - o_x}{d_x}
$$

image-20250626121859841

三维求交

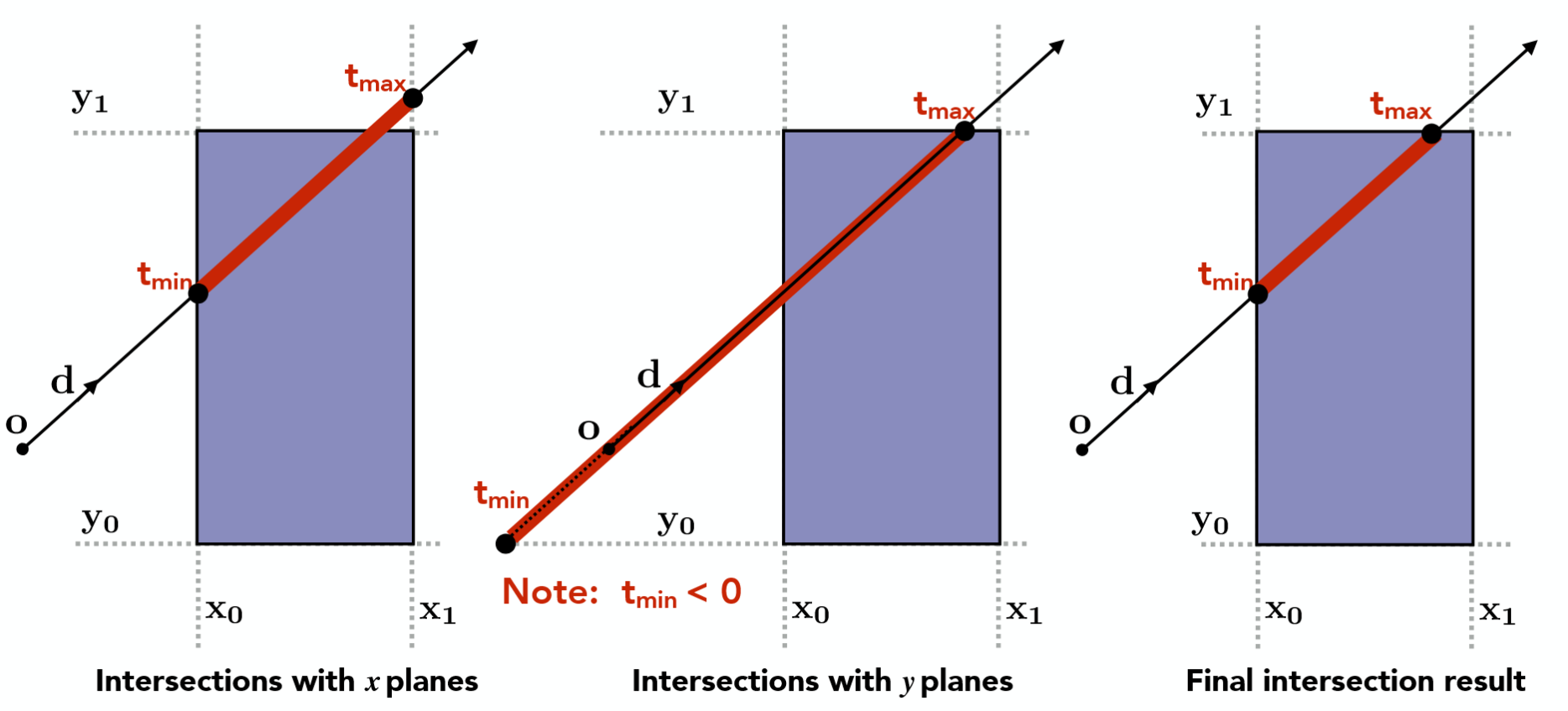
对于每对平面计算出 $t_{\min}, t_{\max}$，可以得到进入时间 $t_{\mathrm{enter}} = \max{t_{\min}}$ 和离开时间 $t_{\mathrm{exit}} = \min{t_{\max}}$。

  • 如果 $t_{\mathrm{enter}} < t_{\mathrm{exit}}$，说明光线或其反向传播线经过了包围盒。
  • 如果 $t_{\mathrm{exit}} < 0$，说明物体在光线的“背后”，反向传播线才能经过包围盒，没有交点。
  • 如果 $t_{\mathrm{exit}} \ge 0 \land t_{\mathrm{enter}} < 0$，说明光源在包围盒内部，有交点。
  • 总结下来的判定条件为 $t_{\mathrm{enter}} < t_{\mathrm{exit}} \land t_{\mathrm{exit}} \ge 0$。

使用包围盒（AABB）加速光线追踪

标准空间网格 Uniform Spatial Grids

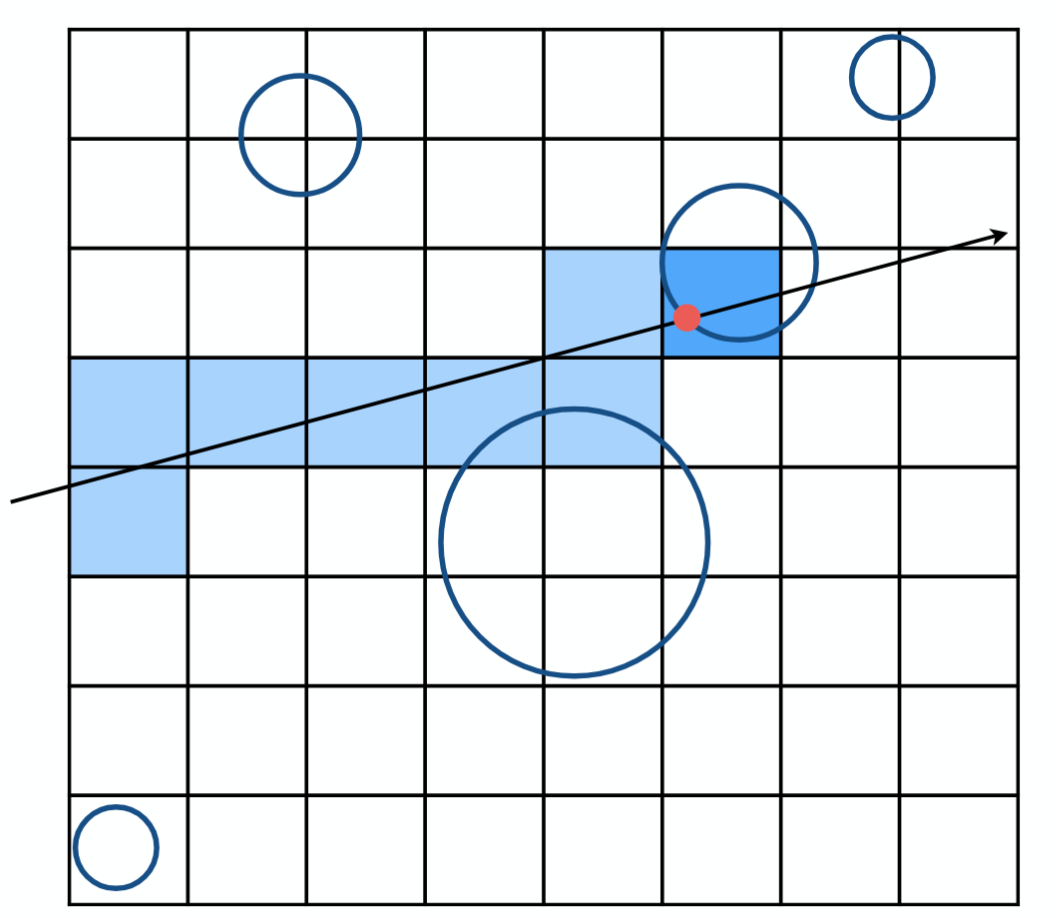
光线在和复杂的物体求交前，先在穿过的网格集合中判断可能求交的物体，以此减少计算量。

预处理

  1. 求出包围盒（AABB）
  2. 创建网格
  3. 对于每个网格，存储穿过了该格的物体列表

查询

  1. 按光线方向遍历穿过的网格
  2. 对于每个网格，对光线和列表里的物体判断是否相交

使用场景

  • 太少的网格起不到加速作用
  • 太多的网格带来多余的光线与网格的计算
  • 经验系数：网格数量 = $C \times$ 物体数量，三维空间中 $C = 27$
  • 高效场景：空间中物体均匀分布
  • 低效场景：空间中出现高密度区域和大片空白区域（teapot in a stadium problem）

image-20250812104054250

空间划分 Spatial Partition

在空间密度不均匀的场景中，我们可以改变空间划分的模式，在物体稀疏的位置使用更大的网格，在物体密集的位置使用更小的网格。

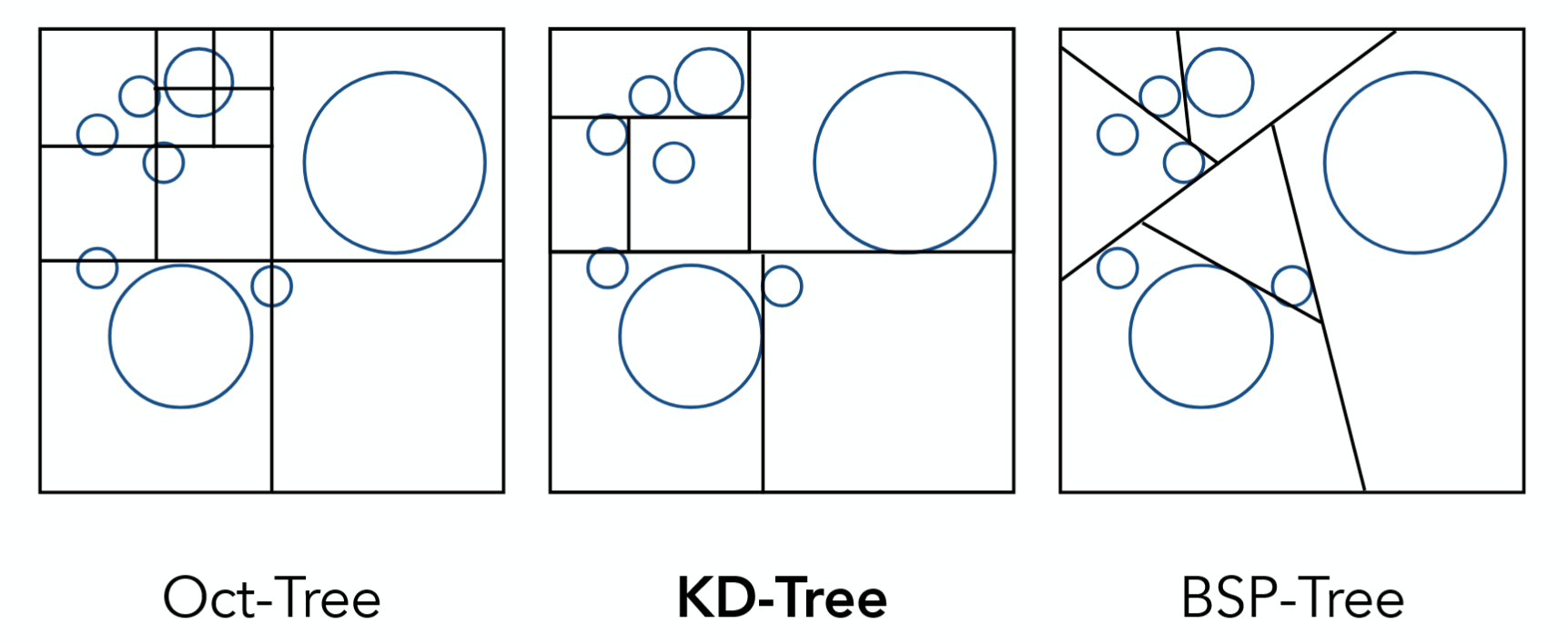
image-20250812110017784

Oct-Tree：八叉树，沿三个轴均分形成八个子空间

KD-Tree：二叉树，沿一个轴分成两个子空间，通常取方差最大的轴

BSP-Tree：二叉树，沿一条直线分成两个子空间，使得两侧的点数相等

KD-Tree

每次沿一个轴划分空间，所以内部节点负责记录划分的轴和具体坐标（例如 $x=2$），叶子节点负责记录穿过的物体列表。

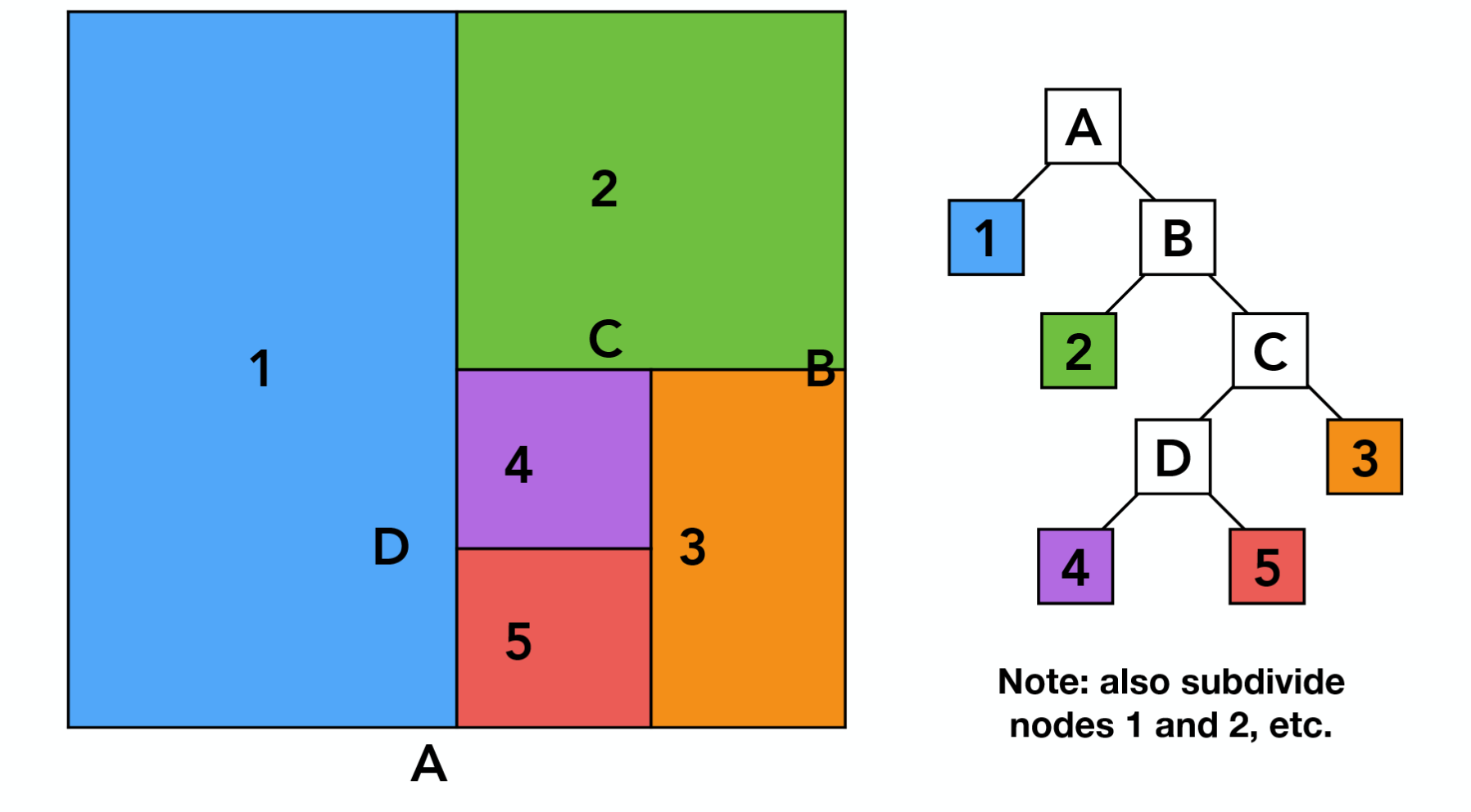
image-20250812112300056

在查询时，我们通过 AABB 的四条边加上内部节点记录的划分线，确定直线是否与左右子空间有交集，有交集的一侧需要递归（可能两侧都要递归）。

KD-Tree 的问题：

  1. 来自空间划分的问题，一个物体会被不同的网格记录，造成重复
  2. 不能判断物体与物体间的相交情况（三角形可能三个顶点都不在需要求交的空间内）

物体划分 Object Partition

Bounding Volume Heirarchy (BVH) 基于物体划分集合，能克服 KD-Tree 的问题。

每次将集合的物体划分为两个子集，划分的策略可以参考KD-Tree，两个子集分别计算包围盒（可能重叠）。

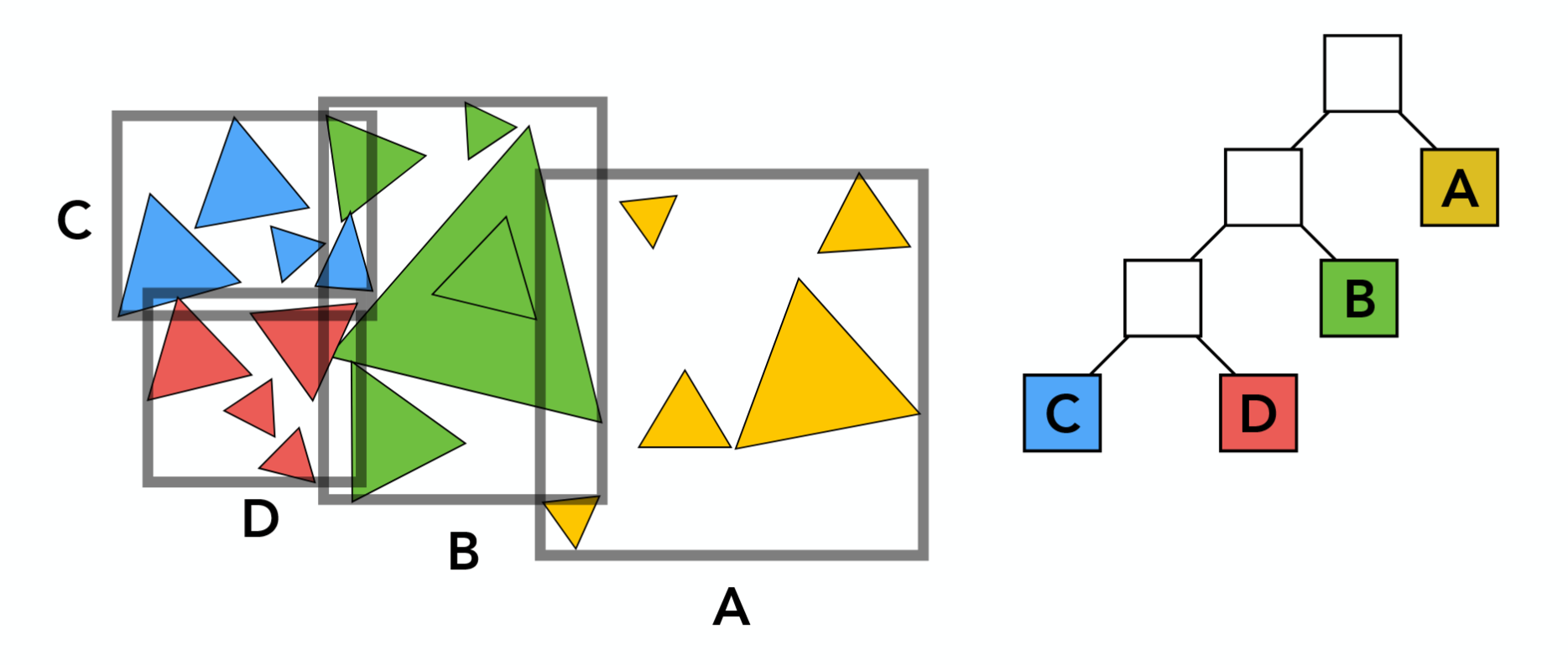
image-20250815152621492

划分技巧

  1. 每一次总沿极差最大的轴划分
  2. 根据坐标的中位数划分物体，用快速划分 $O(N)$ 求中位数
  3. 在节点包含的元素较少（例如 5）时停止

对比

  • 空间划分：
    • 将空间划分为不重合的子空间
    • 一个物体可能在多个子空间中
  • 物体划分：
    • 将物体划分为子集
    • 子集的包围盒可能重合

辐射度量学 Basic radiometry

辐射度量学：

  • 系统地用物理量描述光线，在物理上定义和计算光照
  • 定义了一系列的方法和单位，实现光的不同空间属性
    • radiant flux, intensity, irradiance, radiance
  • 为路径追踪提供基础。

Radiant Energy and Flux (Power)

  • Radiant Energy: 电磁辐射量，用来描述光源辐射的能量，记为 $Q$，单位焦耳 $\mathrm{J}$。

  • Radiant Flux (Power): 电磁功率，也称为光通量，描述单位时间一个曲面辐射、反射、传输或接收的能量，记为 $\Phi \equiv \frac{dQ}{dt}$，单位瓦特 $\mathrm{W}$ 或流明 $\mathrm{lm}$。

Radiant Intensity

定义：单位立体角发射的光功率，记为 $I(\omega) \equiv \frac{d \Phi}{d \omega}$，单位 $\frac{\mathrm{W}}{\mathrm{sr}}$ 或辛德拉 $\frac{\mathrm{lm}}{\mathrm{sr}} = \mathrm{cd}$。

立体角

众所周知，常用弧度定义平面角 $\theta = \frac{l}{r}$，其中 $l$ 为弧长，$r$ 为半径；一个圆的弧度为 $\frac{2\pi r}{r} = 2\pi (\text{radian})$。

推广得到立体角的定义 $\Omega = \frac{A}{r^2}$，其中 $A$ 为面积，$r$ 为半径；一个球的角度为 $\frac{4\pi r^2}{r^2} = 4\pi(\text{steradian})$。

微分立体角

假设一个角由 $(\theta, \phi)$ 表示，对应的微分立体角推导如下。
$$
\mathrm{d}A = (r\mathrm{d}\theta)(r\sin \theta \mathrm{d}\phi)
$$ $$
= r^2 \sin \theta\ \mathrm{d}\theta\ \mathrm{d}\phi
$$ $$
\mathrm{d}\omega = \frac{\mathrm{d}A}{r^2} = \sin \theta \ \mathrm{d}\theta\ \mathrm{d}\phi
$$ $$
\Omega = \int_{0}^{2\pi}\int_{0}^{\pi} \sin \theta \mathrm{d}\theta\mathrm{d}\phi
$$ $$
= 4\pi
$$

和点光源的关系

在点光源外作一个闭合球面，所有的光都恰好穿过一次这个面，那么有
$$
\Phi = \int_{S^2} I \mathrm{d}\omega
$$ $$
\Phi = 4\pi I
$$ $$
I = \frac{\Phi}{4\pi}
$$

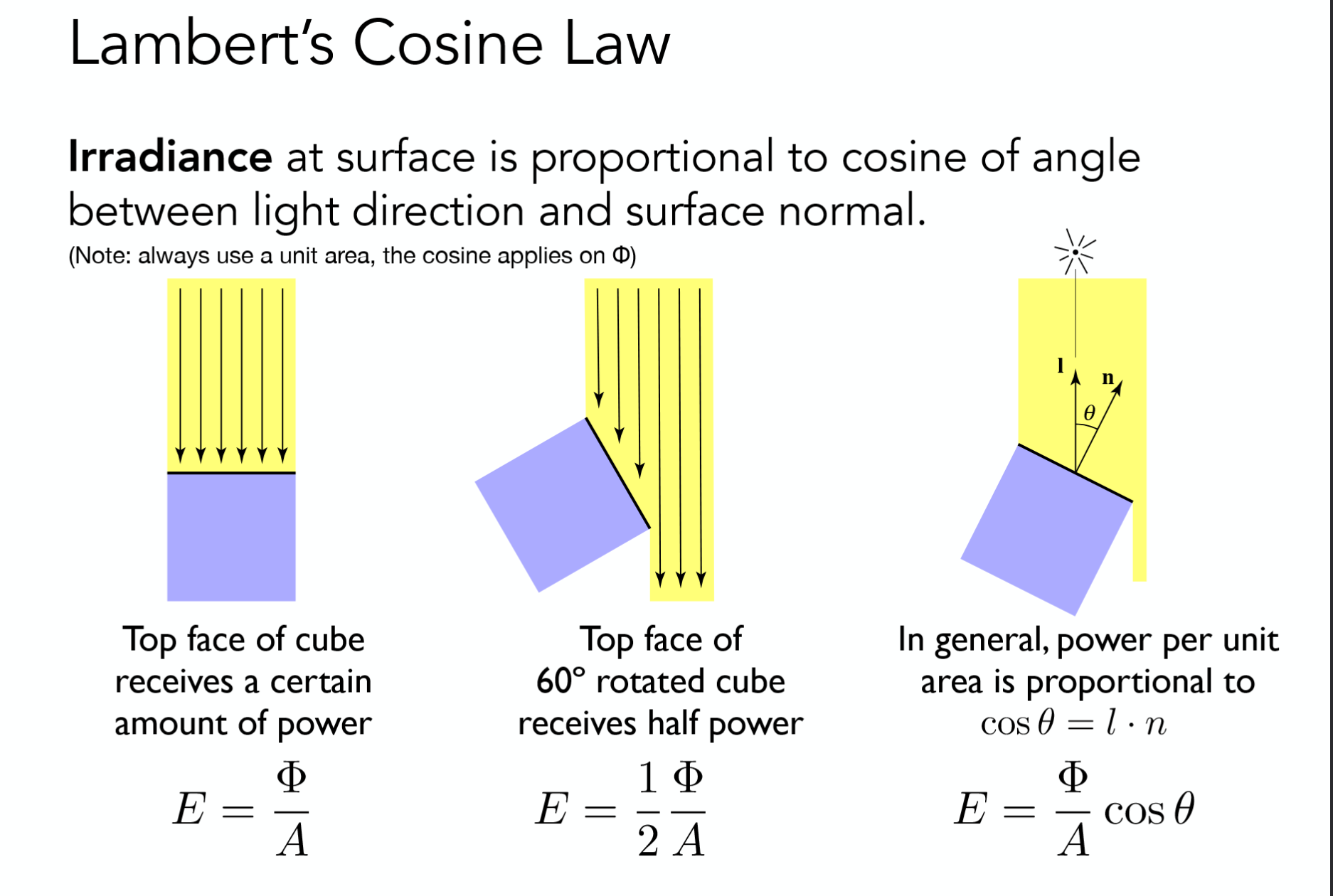
Irradiance

一个表面上，单位面积接收的功率，记为 $E(\mathbf{x}) \equiv \frac{\mathrm{d}\Phi(\mathbf{x})}{\mathrm{d}A}$，单位 $\frac{\mathrm{W}}{\mathrm{m}^2}$ 或拉克丝 $\frac{\mathrm{lm}}{\mathrm{m}^2}=\mathrm{lux}$。

只考虑垂直表面的光线能量，不垂直的根据 $\sin\theta$ 修正。

根据高斯定理，对于点光源外一个球面有 $E = \frac{\Phi}{4\pi r^2}$。

image-20250818170640562

Radiance

定义：光在单位立体角、单位面积上发射、反射、传播或接收的功率，记为 $L$，单位 $\frac{\mathrm{W}}{\mathrm{sr} \ \mathrm{m}^2}$ 或尼特 $\frac{\mathrm{cd}}{\mathrm{m}^2} = \mathrm{nit}$。
$$
L(p, \omega) \equiv \frac{\mathrm{d}\Phi(p, \omega)}{\mathrm{d}\omega\mathrm{d}A\cos\theta}
$$
（$\cos \theta$ 表示投影方向和平面法线方向的夹角）

image-20250818170728967

Intensity, Irradiance and Radiance

  • Radiance = Irradiance per solid angle
  • Radiance = Intensity per projected unit area

光线传播理论 Light Transport

反射方程 Reflection Equation

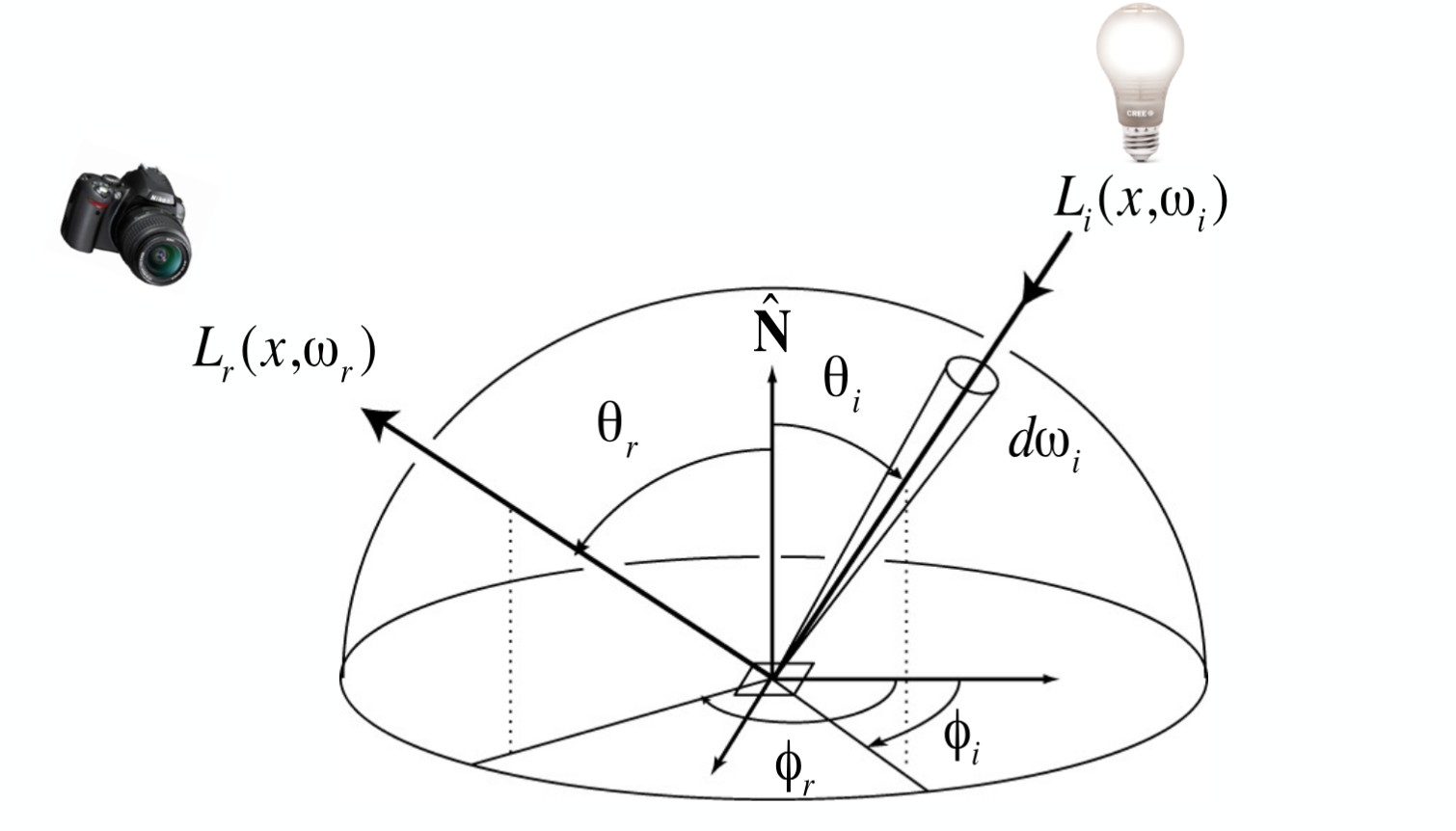
双向反射分布函数 Bidirectional Reflectance Distribution Function (BRDF) 用于描述一个方向的光在一个平面上反射，对于一个给定的反射方向辐射的能量。

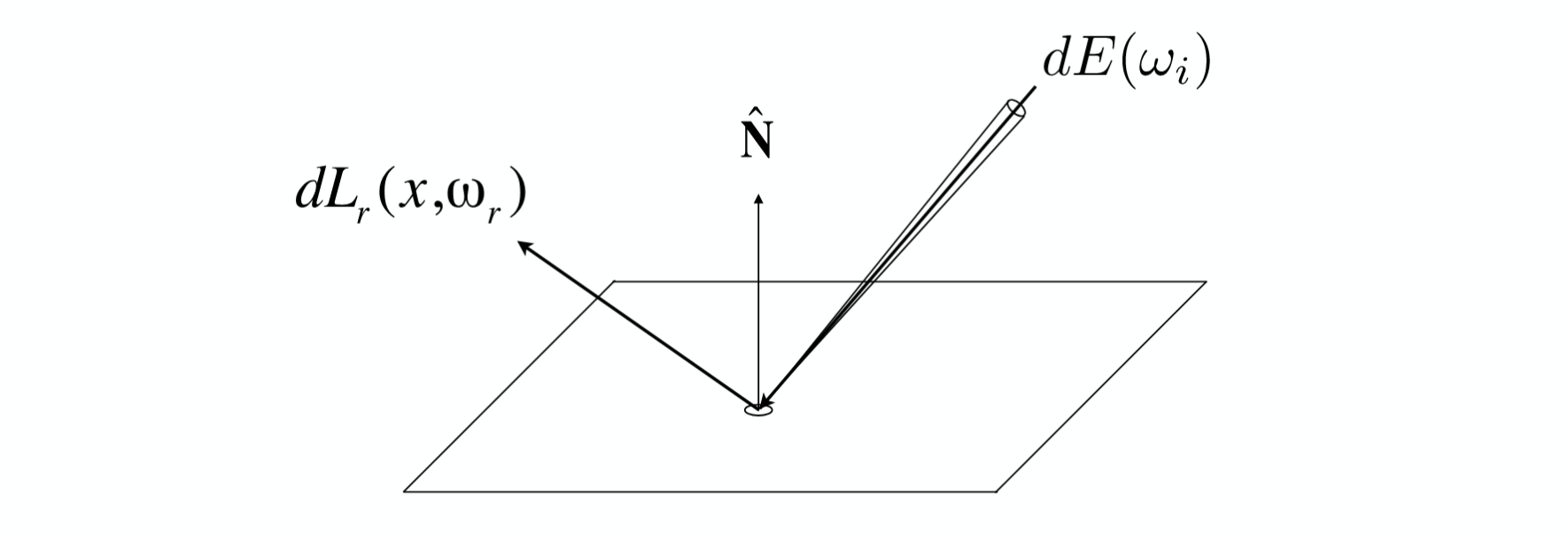
image-20250820141205716

假设光线 $\mathrm{d}E(w_i)$ 以 $\omega_i$ 角度在 $\mathrm{d}A$ 上反射，那么对于反射角度 $\omega_r$ 得到的 Radiance 为 $\mathrm{d}L_r(\omega_r)$。

  • 入射光：$\mathrm{d}E(p, \omega_i) = L(p, \omega_i)\cos \theta_i \mathrm{d}\omega_i$

  • 出射光：$\mathrm{d}L_r(p, \omega_r) = f_r(p, w_i \rightarrow w_r) L_i(p, w_i) \cos \theta_i \mathrm{d} \omega_i$

反射方程如下：
$$
L_r(p, \omega_r) = \int_{H^2}f_r(p, \omega_i \rightarrow w_r) L_i(p, \omega_i) \cos \theta_i \mathrm{d} \omega_i
$$

image-20250820143608791

渲染方程 Redering Equation

考虑真实情况下，任何的出射光都可能成为一个平面的入射光，同时物体自己也能发光，渲染方程如下：
$$
L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{\Omega^+} L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) \mathrm{d} \omega_i
$$
与反射方程的联系：$\Omega^+$ 和 $H^2$ 都表示半球，$n \cdot \omega_i = \cos \theta_i$。

注意：所有的角度方向都朝外，入射光的方向也由平面作起点。

全局光照 Global Illumination

全局光照可以从求解渲染方程的角度理解：
$$
L_r(x, \omega_r) = L_e(x, \omega_r) + \int_{\Omega} L_r(x^\prime, -\omega_i) f(x, \omega_i, \omega_r) \cos \theta_i \mathrm{d} \omega_i
$$
其中，$L_r$ 是未知量，其余的是已知量。

可以简化为第二类 Fredholm 积分方程：
$$
l(u) = e(u) + \int l(v) K(u, v) \mathrm{d} v
$$
可以被离散化为三个向量的方程，并应用二项式定理：
$$
L = E + KL
$$ $$
IL - KL = E
$$ $$
(I-K)L = E
$$ $$
L = (I - K)^{-1}E
$$ $$
L = (I + K + K^2 + K^3 + \cdots) E
$$
这样就粗略地解出了光照的表达式。

蒙特卡洛积分 Monte Carlo Integration

为什么要用

蒙特卡洛积分用于计算一个复杂函数的定积分，这里的函数不能得出解析式。

方法

在区间内随机采样 $x$，每次取样 $f(x)$ 作为区间的高，用长方形近似区间面积，所有采样的平均值为积分的近似值。

Uniform Monte Carlo Estimator

使用均匀随机采样 $X_i \sim p(x) = \frac{1}{b - a}$，估计的结果为

$$
F_N = \frac{b - a}{N} \sum_{i=1}^{N} f(X_i)
$$

一般写为

$$
\int f(x) \mathrm{d}x = \frac{1}{B} \sum_{i = 1}^{N} \frac{f(X_i)}{p(X_i)} \quad X_i \sim p(x)
$$

路径追踪 Path Tracing

Whitted-Style 的问题

image-20250822150030714

不同材质导致反射的效果不同，不是完全的镜面反射会产生模糊。

image-20250822151807849

观察天花板，有全局光照后才有光照；

观察中间两个长方体，反射出墙壁的颜色，这种现象称为 color bleeding。

蒙特卡洛解渲染方程

接下来不再对自发光和反射光作区分，方程为
$$
L_o(p, \omega_o) = \int_{\Omega^+} L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) (n \cdot \omega_i) \mathrm{d} \omega_i
$$

直接光照

考虑渲染一个像素，有一个面光源，只有直接光照：

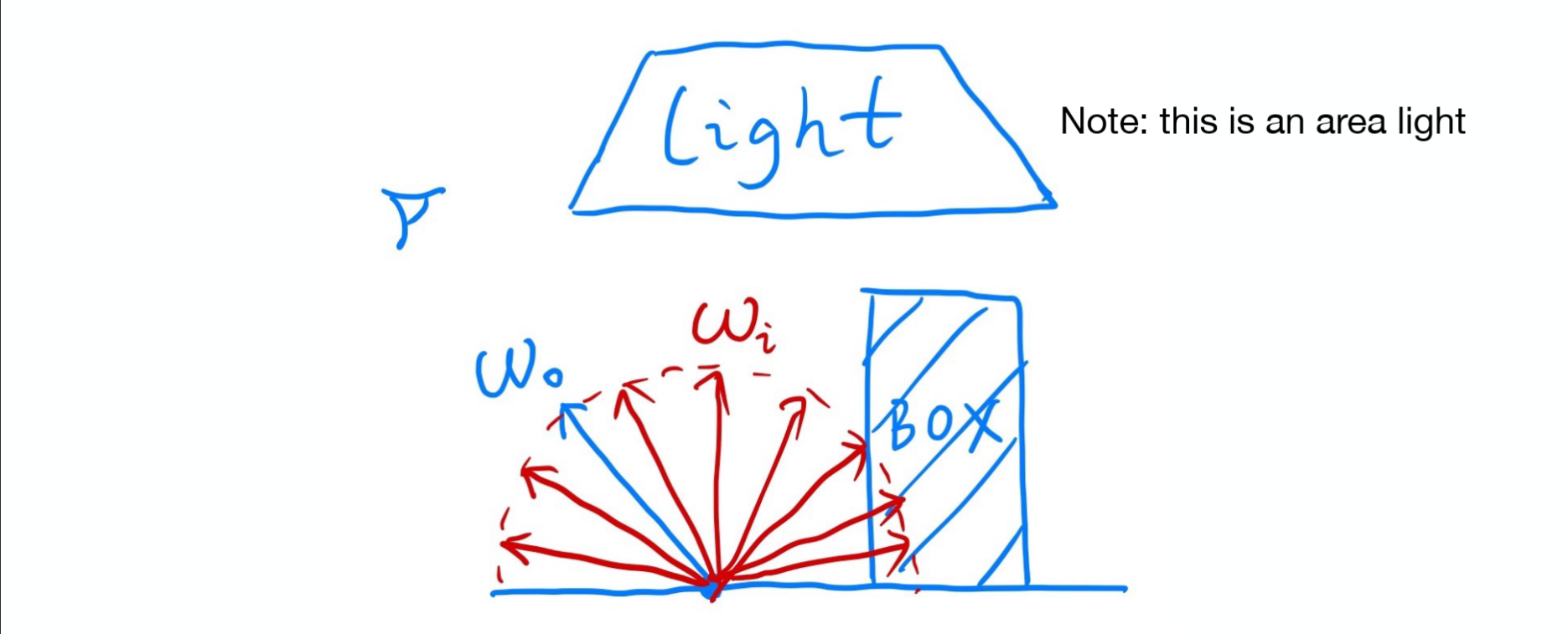
image-20250822152216311

分析 $\int_a^{b} f(x)\mathrm{d}x = \frac{1}{N} \sum_{i=1}^{N} \frac{f(X_k)}{p(X_k)}\quad x_k \sim p(x)$：

被积函数为 $f(x) = L_i(p, \omega_i) f_r(p, \omega_i, \omega_o) (n \cdot \omega_i)$；

概率密度函数为 $p(\omega_i) = \frac{1}{2\pi}$（均匀采样）；

那么估计式为：
$$
L_o(p, \omega_o) \simeq \frac{1}{N}\sum_{i = 1}^{N} \frac{L_i(p, \omega_i) f_r(p, \omega_i, \omega_o)(n \cdot \omega_i)}{p(\omega_i)}
$$
算法如下：

Function shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
    Return Lo

间接光照

假设两个点 $P, Q$，现在考虑 $P$ 从 $Q$ 接收的光照。

因为 $Q$ 点的光照也是来自于光源，可以把 $P$ 点视为相机，计算 $Q$ 的直接光照，再带入式子。

Function shade(p, wo)
    Randomly choose N directions wi~pdf(w)
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo
问题
  1. 递归导致需要计算的光线数量太多（指数级增长）
    1. $N = 1$ 称为路径追踪 path tracing，可以避免膨胀
    2. 一个像素点也代表多个方向，多次以不同的方向 shade 再平均可以产生更好的效果
  2. 会产生无限递归
    1. 俄罗斯轮盘赌 Russian Roulette：假设一个概率 $P$，我们以 $P$ 概率打出一条光线，得到 $L_o$，返回 $L_o / P$；以 $(1 - P)$ 的概率不打出光线，返回 $0$；这样期望的结果为 $E = P \cdot \frac{L_o}{P} + (1-P) \cdot 0 = L_o$。

改进后的代码如下：

Function shade(p, wo)
    P_RR = a fixed probability
    Randomly choose 1 num ksi ~ uniform dist. in [0, 1]
    If ksi > P_RR
        Return 0.0
    Randomly choose 1 direction wi ~ pdf(w)
    Trace a ray r(p, wi)
    If r hit the light
        Return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
改进方案的效果

改进方案效率较低：在 Sample per Pixel （单像素 shade 方向数量）较低的情况下产生大量噪点；较高的情况下会产生很多浪费，只有少部分的光线能到达光源。

光源采样

为了减少光线的浪费，我们可以在光源上采样 $\mathrm{d}A$，这样每条光线都能到达光源。

但是渲染方程在物体的表面半球上积分 $\mathrm{d}\omega$，为了在光源上采样需要改写为在光源的表面上积分，也就是找到 $\mathrm{d}\omega$ 和 $\mathrm{d}A$ 的代数关系。

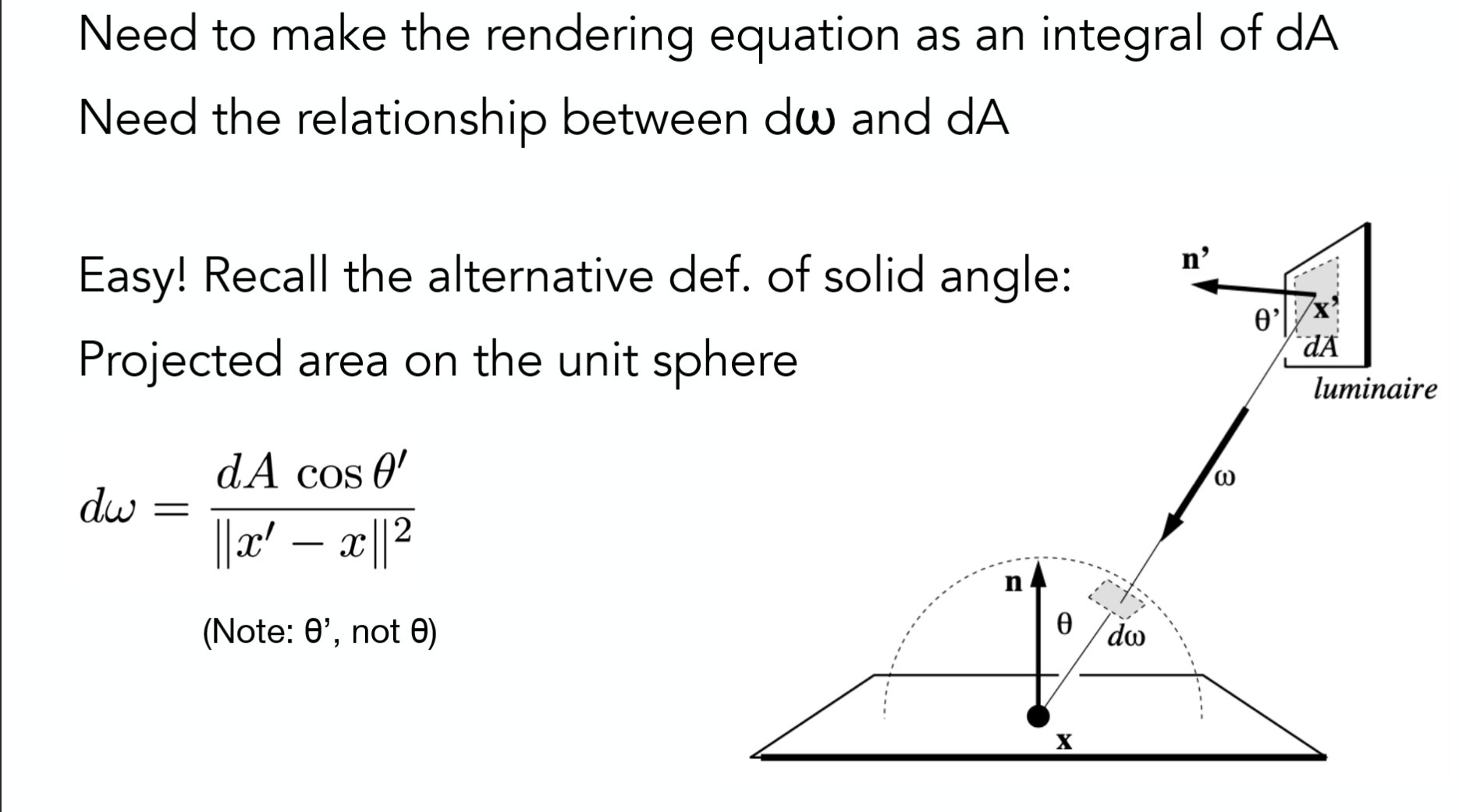
image-20250822162409541

由上图可知
$$
\mathrm{d} \omega = \frac{\cos\theta^\prime \ \mathrm{d} A}{||x^\prime - x||^2}\
p(x) = \frac{1}{A}
$$
渲染方程变为
$$
L_o(x, \omega_o) = \int_A L_i(x, \omega_i) f_r(x, \omega_i, \omega_o) \cdot \frac{\cos \theta \cos \theta^\prime}{||x^\prime - x||^2} \mathrm{d}A
$$
光线传播拆分为了两部分：

  1. 来自光源（在光源上采样，不使用 RR）
    1. 注意：需要判定光线是否被其他物体遮挡
  2. 来自其他物体（沿用之前的方法，使用 RR）
Function shade(p, wo)
    // sample from light source
    Uniformly sample the light at x` (pdf_light = 1 / A)
    Trace a ray t(p, uniform(x` - p))
    If t is not blocked until p
        L_dir = L_i * f_r * cos(theta) * cos(theta`) / |x` - p|^2 / pdf_light
    Else
        L_dir = 0.0
    // RR
    P_RR = a fixed probability
    Randomly choose 1 num ksi ~ uniform dist. in [0, 1]
    If ksi > P_RR
        Return L_dir
    // sample indirect light
    Randomly choose 1 direction wi ~ pdf(w) (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    If r hit a non_emitting object at q
        L_indir = shade(q, -wi) * f_r * cos(theta) / pdf_hemi / P_RR

    Return L_dir + L_indir

没有涉及到的内容

  • 均匀采样单位角
    • 如何随机，以及计算函数值
  • 蒙特卡洛允许任意的概率密度函数
    • 什么函数最优？重要性采样 importance sampling问题
  • 随机数的质量好坏
    • 低差异度序列 low discrepancy sequences 有很好的性质
  • 多种采样方法的结合
  • 为什么平均是对的
    • pixel reconstruction filter
  • 像素的 Radiance 是颜色吗？
    • 不是，需要经过转换和伽马矫正 gamma correction
Bounding VolumeCGComputer GraphicsGeometryGlobal IlluminationIrradianceMonte Carlo IntegrationPath TracingRadianceRadiant IntensityRadiometryRay TracingThe Rendering EquationWhitted-Style光线追踪全局光照渲染方程计算机图形学路径追踪辐射度量学
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																				
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇