本文深入解析计算机图形学中的着色技术,涵盖Blinn-Phong反射模型、漫反射与高光项计算、着色频率(Flat/Gouraud/Phong Shading)及图形管线流程。探讨纹理映射的核心方法,包括Mipmap、各向异性过滤、位移贴图,以及三维纹理应用。结合重心坐标插值与Shader编程实例,为实时渲染与材质表现提供实践指导。(Generated by DeepSeek r1)
着色
什么是着色
韦氏词典上 Shading 的意思如下:
shad·ing, [ˈʃeɪdɪŋ], noun
The darkening or coloring of an illustration or diagram with parallel lines or a block of color.
一般而言,指根据光源画出物体的亮暗关系、颜色变化等内容,本课程中简化为对物体应用不同材质的过程。
简单着色模型
以 Blinn-Phong Reflectance Model 为例。
我们从计算特定点向相机反射的光线开始,而点在足够小的范围内总可以认为是一个反射平面(面元)。一些需要的参数:
- 观察者方向 $\vec v$
- 反射面法线 $\vec n$
- 光线方向 $\vec l$,可能是一个集合
- 着色点本身的性质(颜色、材质亮度等)
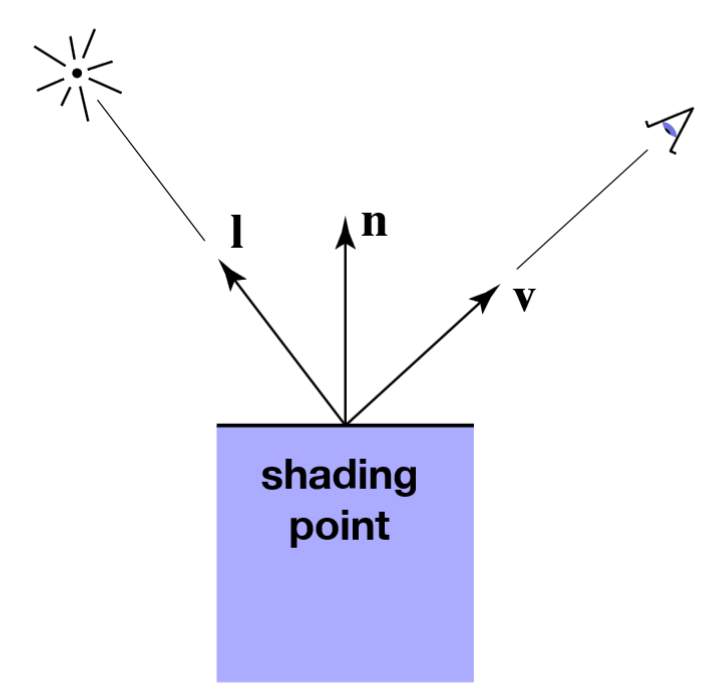
注意此处并不关心光线是否被遮挡,也就是说不考虑遮挡导致的阴影。
漫反射
反射光线均匀地扩散,能量(亮度)均分。
对于一个面元,设垂直接收光的能量为 $I_0$,则一般情况下接收的光强为 $I = I_0 \cos \theta = I_0 \vec n \cdot \vec l$。(Lambert's cosine law)
考虑光的发散,此时对于以点光源为中心的球壳,壳上每一点到中心的时间相等,所以不但壳上各点光强相等,而且球壳上光强的和应该是与距离无关的常量,所以有 $r^2 I_r = R^2 I_R$。
合成一下,假设我们知道点光源 $r = 1$ 时的光强 $I$ 和到着色点的距离 $r$,以及 $\vec n$、$\vec l$,材质对光照的影响 $k_d$,那么有
$$
L_d = \frac{k_d I}{r^2} \max(0, \vec n \cdot \vec l)
$$
$k_d$ 的意义:材质对不同光线的反射强度有差异,导致一些波段的光线被吸收,形成了颜色等材质性质。

简单着色模型
高光项
什么情况下能看到高光?物体比较光滑,大部分的反射光线分布在较小的角度范围内。
Blinn-Phong 模型利用的一个发现:当 $\vec v$ 和镜面反射方向接近时,$\vec n$ 方向和“半程向量” $\vec h$ 很接近,其中 $\vec h = \dfrac{\vec v + \vec l}{||\vec v + \vec l||}$。
这样判定是否能看到高光就能转换为判断 $\vec n$ 和 $\vec h$ 是否足够接近。这里忽略了吸收比率的影响($L_d$ 中的 $\vec n \cdot \vec l$)。
$$
L_s = \frac{k_s I}{r^2} \max(0, \vec n \cdot \vec h)^p
$$
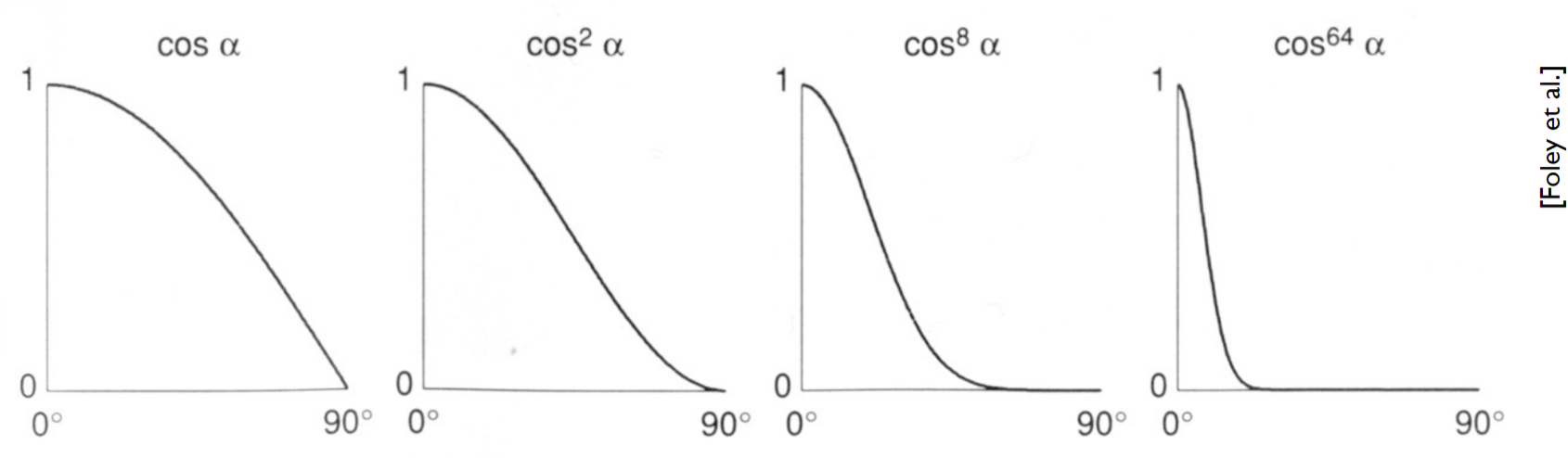
为什么有一个指数 $p$?这是为了限制夹角余弦,以限制分布角度范围的,正常情况下 $p \in [100, 200]$。

环境光项
有些光线可以经过多次反射打在着色点上,使得物体上一些本是阴影的区域能被看见。
这些光线的传播路径非常复杂,所以 Blinn-Phong 模型粗略地假设了所有位置接收到相同的环境光照。
$$
L_a = k_a I_a
$$
将 $L_d, L_s, L_a$ 三项相加即可得到光照。

着色频率
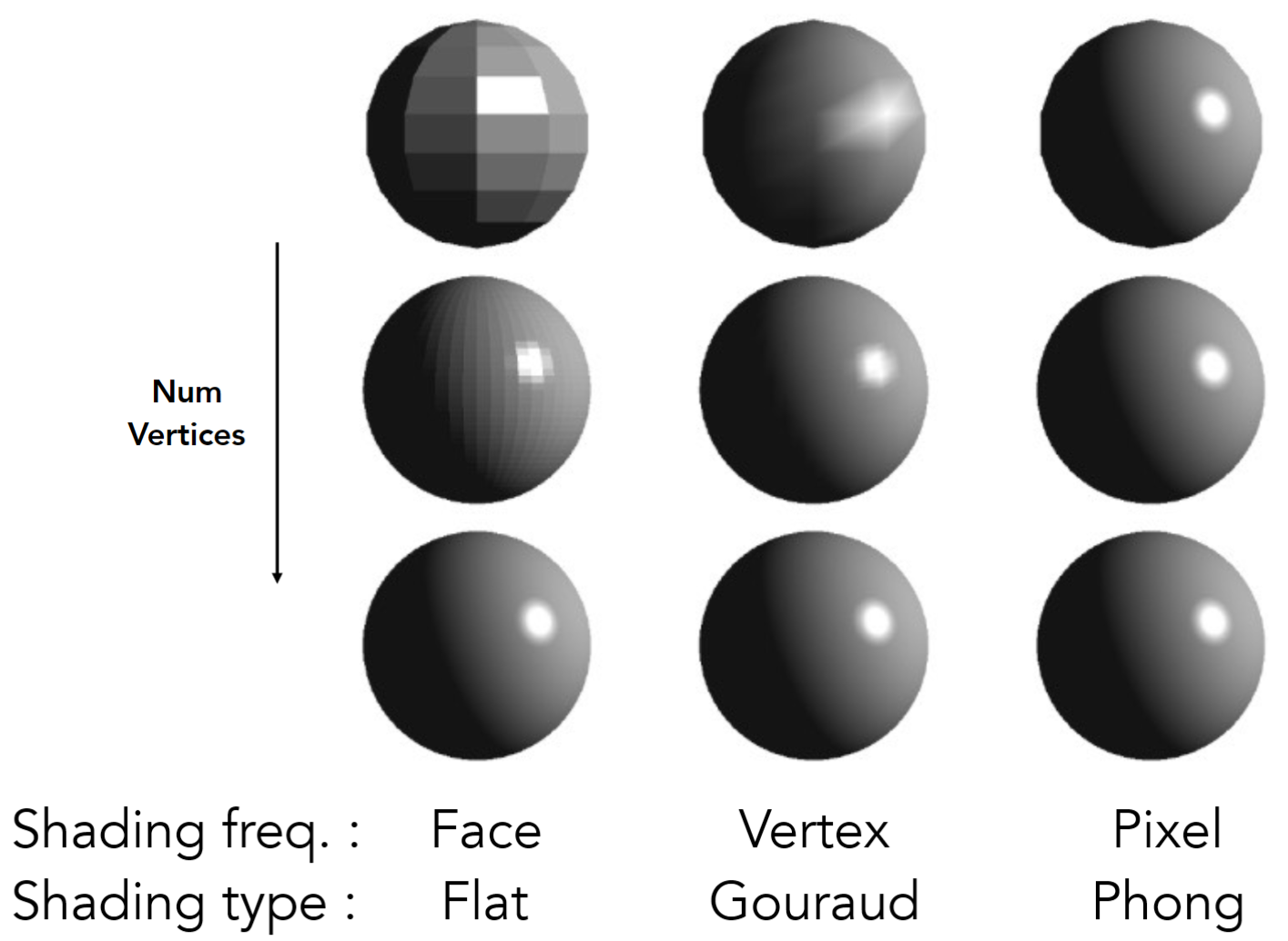
即使使用完全一样的模型,不同的着色策略会影响最终形成的图像细节。
左:每个平面取一个点的法线,计算着色;
中:取每个顶点的法线计算着色,在三角形内部用颜色插值计算;
右:取每个顶点的法线,在三角形内计算每个像素的法线,计算着色。

Flat Shading
对于每个三角形,用两边叉积计算法线,然后着色。对于三角形内部,认为着色效果不变。
当然对光滑物体效果不好。
Gouraud Shading
对于每个顶点求法线(?),对每个顶点着色。对于三角形内部,通过插值计算颜色。
Phong Shading
对于每个顶点求法线。在三角形内部,对像素通过插值计算法线,然后着色。
注意和 Blinn-Phong 模型区分开。
如何计算点的法线
对于所举例子,一个天然的想法是,既然知道我们要表示一个球,那么顶点处的径向就是法线。
但大部分物体都不代表一个规则的理想物体,所以猜测的方法不够通用。
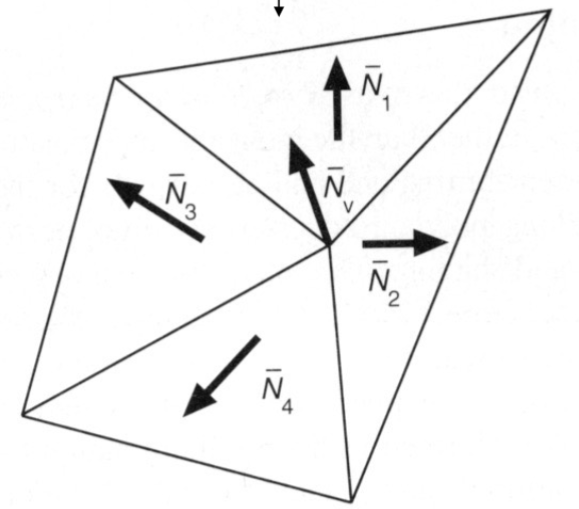
另一个简单的想法是,将顶点相邻的面的法线相加。目前通用的方法:按照面积将顶点相邻的多边形面的法线加权平均。
$$
\vec N_v = \frac{\sum_i \vec N_i}{\left | \left | \sum_i \vec N_i \right | \right |}
$$
图形管线
图形管线是前面我们图形显示的操作的总称。
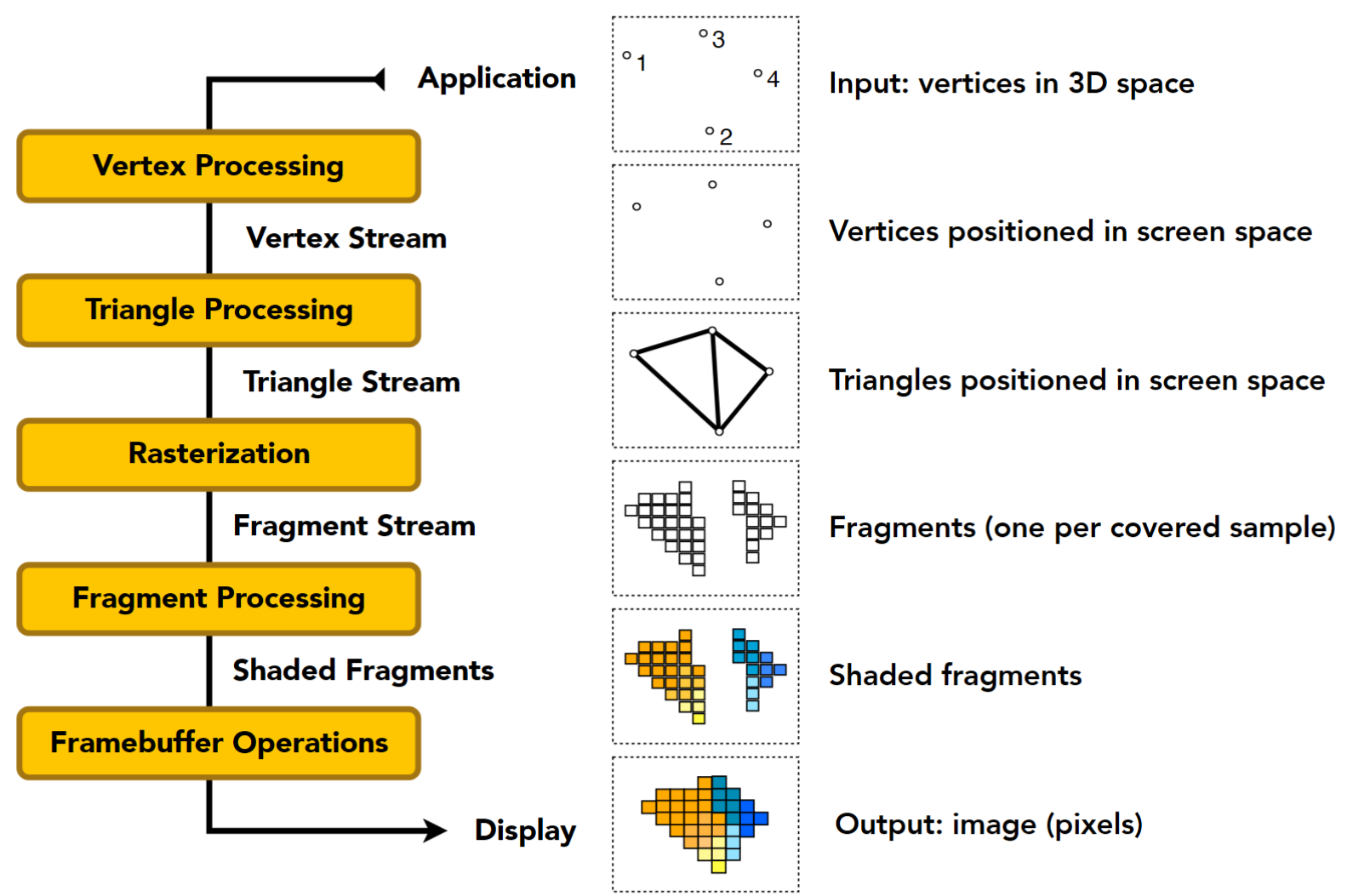
现代 GPU 显示一个由顶点和连线关系定义的物体的基本流程如上。其中大部分已经固化到硬件上,留下了顶点着色等部分可编程。
控制顶点和像素如何进行着色的代码称为 Shader,是实时渲染的重要部分。
通过 API 编程
在 shader 中只负责一个着色点的着色操作。分为 vertex shader 和 fragement / pixel shader。
下面是 OpenGL 着色语言(GLSL)编写的 fragment shader 程序片段:
uniform sampler2D myTextrue;
uniform vec3 lightDir; // 光照方向 l
varying vec2 uv;
varying vec3 norm; // 顶点法线的插值结果 n
void diffuseShader(){
vec3 kd;
kd = texture2d(myTexture, uv); // 漫反射系数
kd *= clamp(dot(-lightDir, norm), 0.0, 1.0); // 乘上 n 和 l 叉积
gl_FlagColor = vec4(kd, 1.0);
}推荐的练习网站:shadertoy.com
纹理映射
目前为止我们讨论的都是黑白图像,尚未考虑物体的实际颜色。
那么就需要一种方法来定义物体的颜色,并在着色时正确应用。这个过程称为纹理映射 texture mapping。
纹理
任何一个三维物体,其表面总可以通过拉伸、裁剪、拼接放在一张图上。那么我们将这张图称为物体的纹理。
物体的任意点和纹理的点产生映射关系,这样在着色时就能在图上找到着色点的实际颜色。对应关系的建立是另外的重大工程。
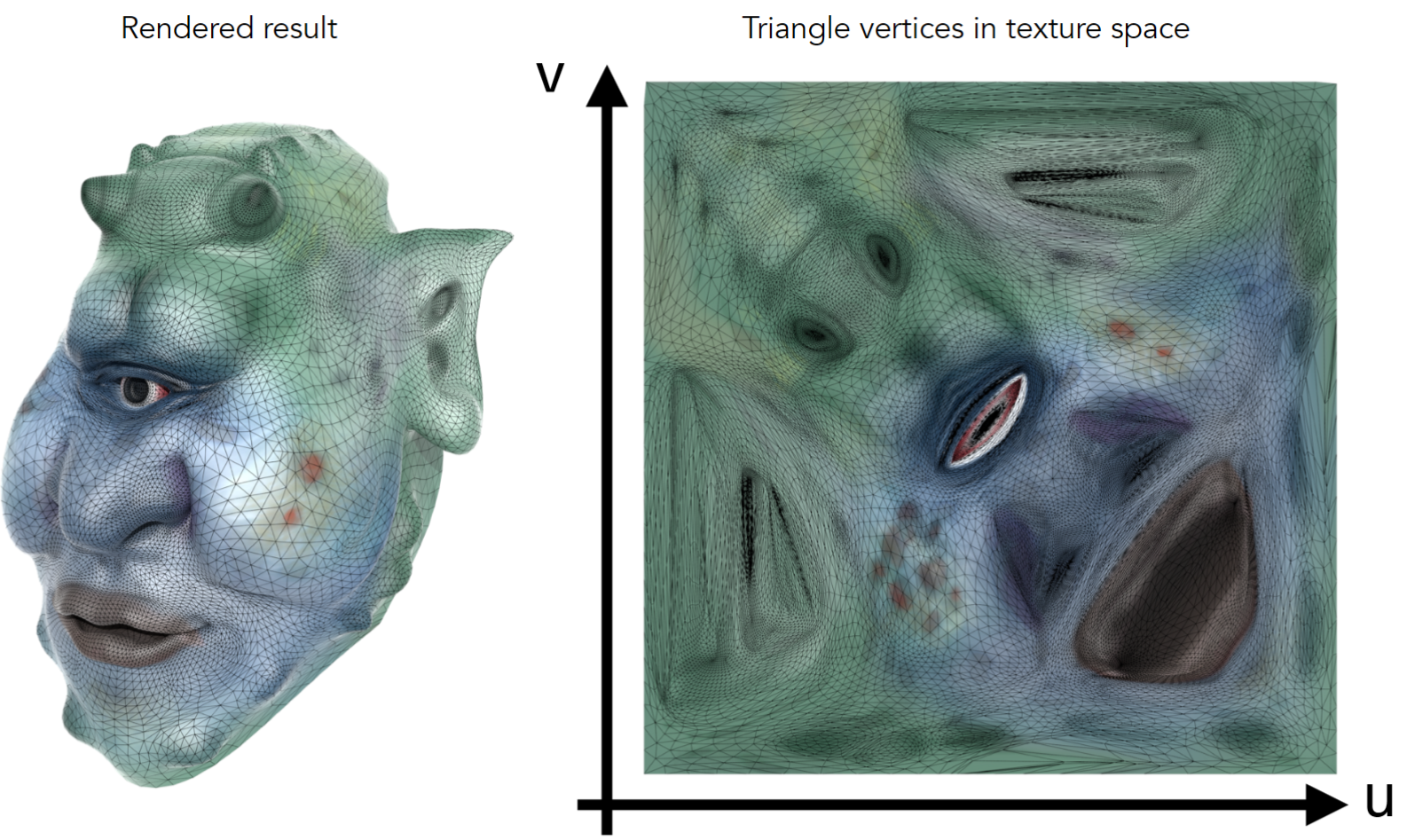
复用性
纹理具有复用性:场景效果可以由一块纹理重复拼接而成。
无缝衔接的纹理的设计也是重大工程。
重心坐标
给定三角形顶点的函数值,为了在三角形内平滑地过渡,我们需要插值。
可以插值的属性:贴图坐标、颜色、法线等
而通过重心坐标可以解决插值问题。
表示方法
对于一个三角形 $ABC$ 和点 $(x, y)$,有 $(x, y) = \alpha A + \beta B + \gamma C$,其中 $\alpha + \beta + \gamma = 1$;且当 $(x, y) \in \triangle ABC$ 时,有 $\alpha, \beta, \gamma \ge 0$。
那么 $(\alpha, \beta, \gamma)$ 就称为 $\triangle ABC$ 的重心坐标 Barycentric coordinates。
三个系数由面积比确定:
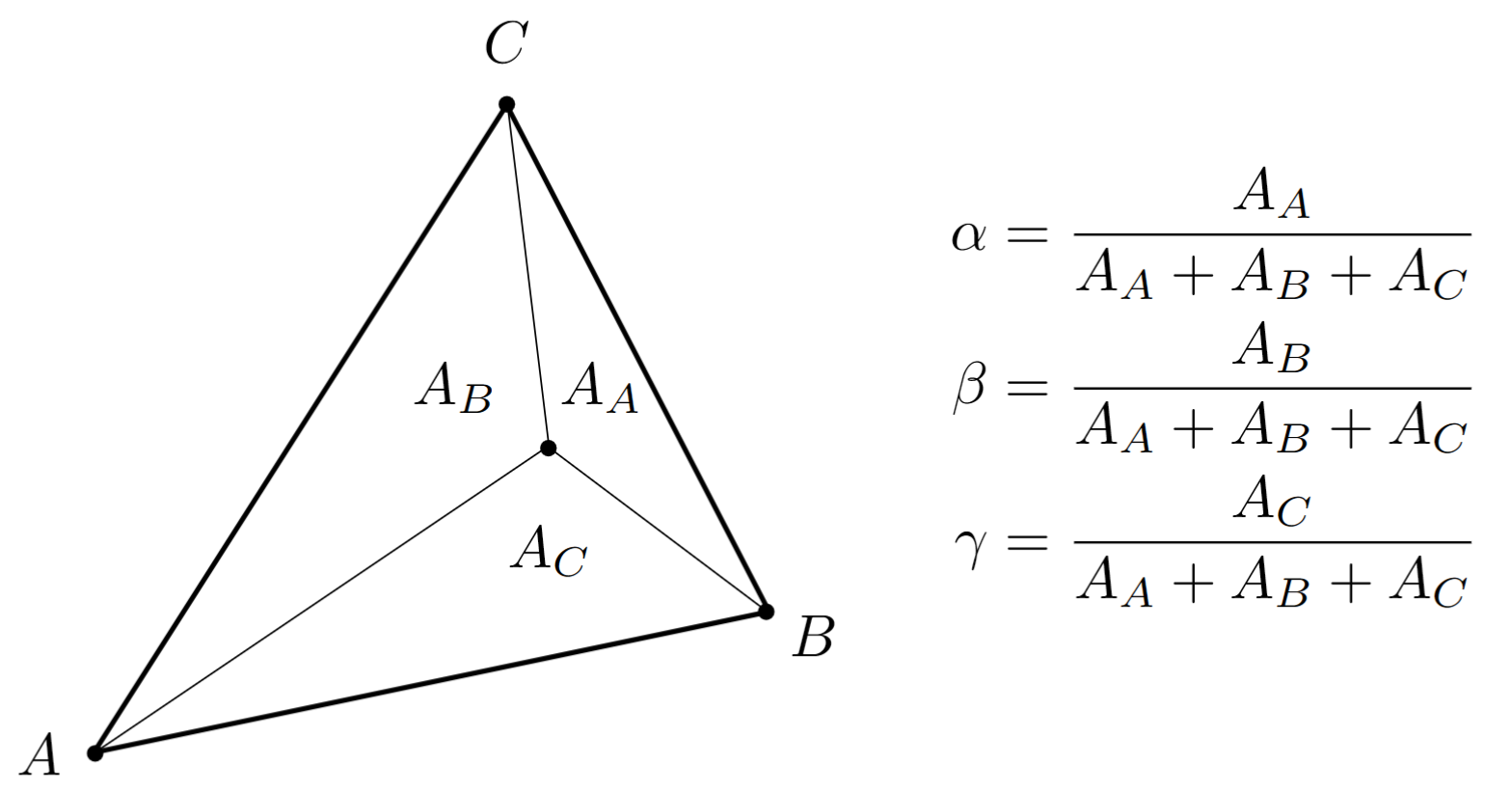
导出表达式:
$$
\alpha = \frac{-(x - x_B)(y_C - y_B) + (y - y_B)(x_C - x_B)}{-(x_A - x_B)(y_C - y_B) + (y_A - y_B)(x_C - x_B)}
$$ $$
\beta = \frac{-(x - x_C)(y_A - y_C) + (y - y_C)(x_A - x_C)}{-(x_B - x_C)(y_A - y_C) + (y_B - y_C)(x_A - x_C)}
$$ $$
\gamma = 1 - \alpha - \beta
$$
任何一个点属性的插值也 应该由重心坐标将端点属性线性组合到该点上:$V = \alpha V_A + \beta V_B + \gamma V_C$。
缺点:没有投影不变性,对于三维的物体应该先插值再投影。
纹理放大
在纹理图片的分辨率小于实际需要时,就需要纹理放大。
纹理上的一个像素称为纹理元素 texel。
当像素在建立映射时,因为纹理分辨率太小导致映射的坐标不是整数,这时候需要额外处理。
双线性插值 Bilinear
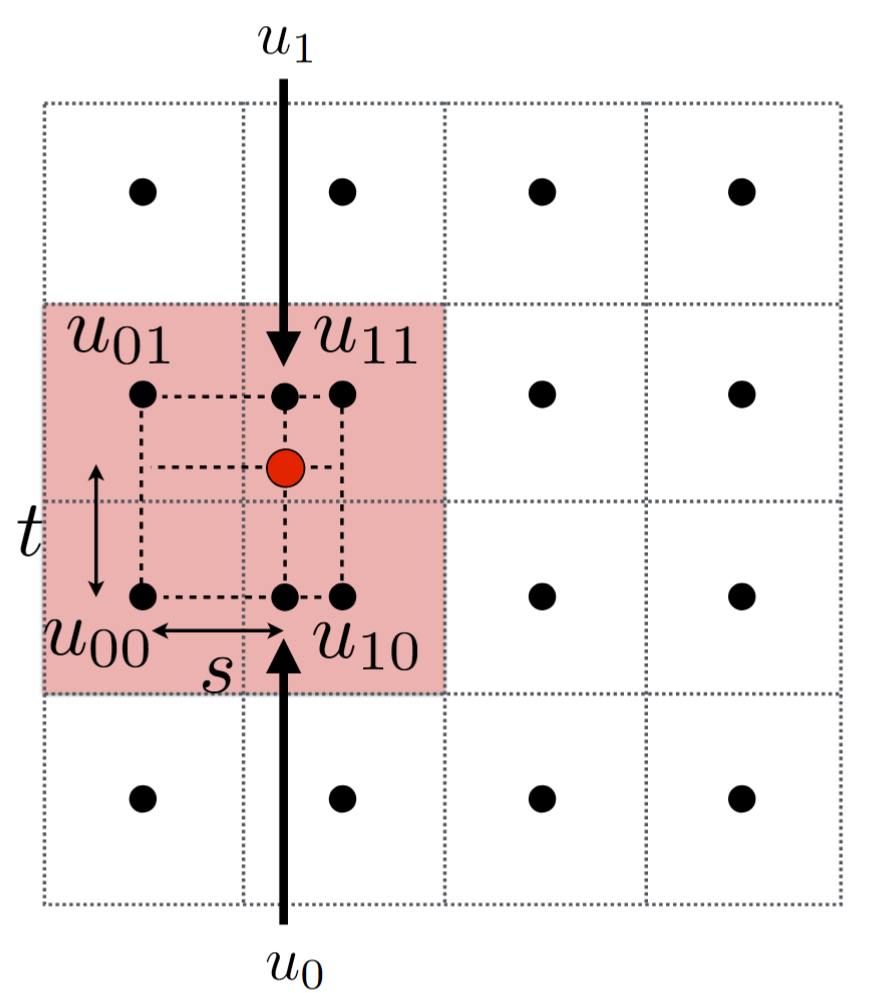
对于一点 $(x, y)$,我们先找到离它最近的四个点,其颜色记作 $u_{xy} (x, y \in {0, 1})$。
然后再定义线性插值 $\mathrm{lerp}(x, v_0, v_1) = v_0 + x(v_1 - v_0)$,$x$ 为比例。
这样先做水平方向的插值 $u_0 = \mathrm{lerp}(s, u_{00}, u_{10})$ 和 $u_1 = \mathrm{lerp}(s, u_{01}, u_{11})$,
再做竖直方向的插值 $f(x, y) = \mathrm{lerp}(t, u_0, u_1)$,就可以得到一个插值后的颜色。
双三次插值 Bicubic
原理和双线性插值相同,只不过将邻域扩大到周围 16 个点,每次使用 4 个点做三次多项式的插值。

纹理缩小
如果纹理图分辨率太高,又会出现光栅化时的走样:摩尔纹 + 锯齿。
原因:不同的位置的像素,代表了不同大小的纹理,使用中心表示不总是准确的。
一个简单的处理方法是将像素代表的纹理区域求平均,这样就需要区间查询。
三线性插值
引入 Mipmap,允许做范围查询,特点是快速、近似、仅正方形。
对于一张图,我们提前将其降低分辨率,得到一系列图片:Level $D$ 的分辨率为 $\left(\dfrac{L}{2^D}\right)^2$,$L$ 为 Level 0(原图)分辨率。
由级数求和的知识可知,总共增加了 $\frac{1}{3}$ 的额外存储开销。

我们还要知道一个像素对应的贴图范围(边长)是多少,可以通过求邻域距离实现:
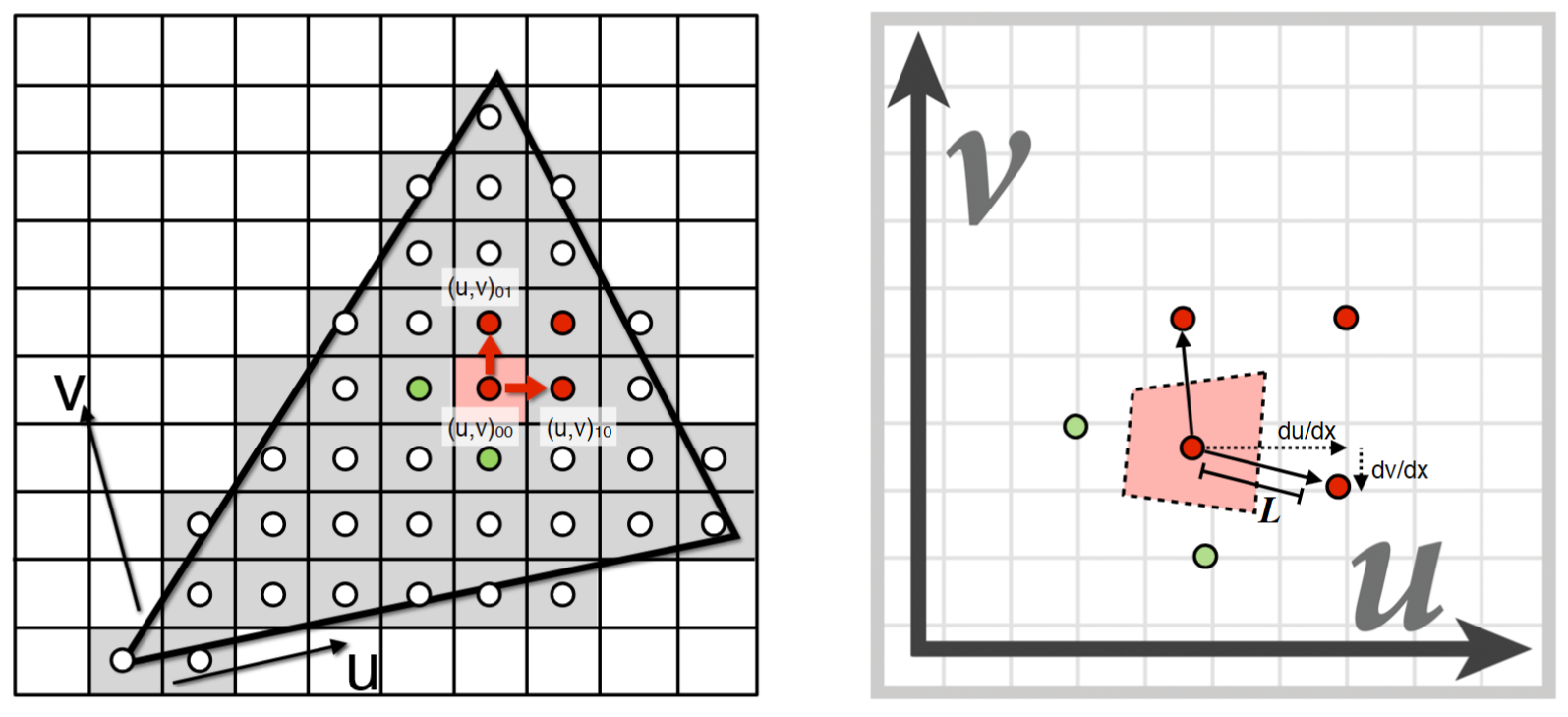
$$
L = \max \left( \sqrt{\left(\dfrac{\mathrm{d}u}{\mathrm{d}x}\right)^2 + \left(\dfrac{\mathrm{d}v}{\mathrm{d}x}\right)^2}, \sqrt{\left(\dfrac{\mathrm{d}u}{\mathrm{d}y}\right)^2 + \left(\dfrac{\mathrm{d}v}{\mathrm{d}y}\right)^2} \right)
$$
在 $D = \log_2 L$ 层上,这个区域就会压缩成一个像素,那么在其位置查询就可以。但是这样做对于绝大部分位置 $D \notin \N$,我们就需要前后两层做插值。
假设我们现在 有 $T < D < T + 1, T \in \N$。我们先在 $T$ 和 $T + 1$ 层做插值 $f_T$ 和 $f_{T+1}$,再用这两个值做线性插值。
该方法称为三线性插值 Trilinear。
因为涉及 Mipmap 的近似、线性插值的近似,所以在远处的图像会有过度模糊的问题。
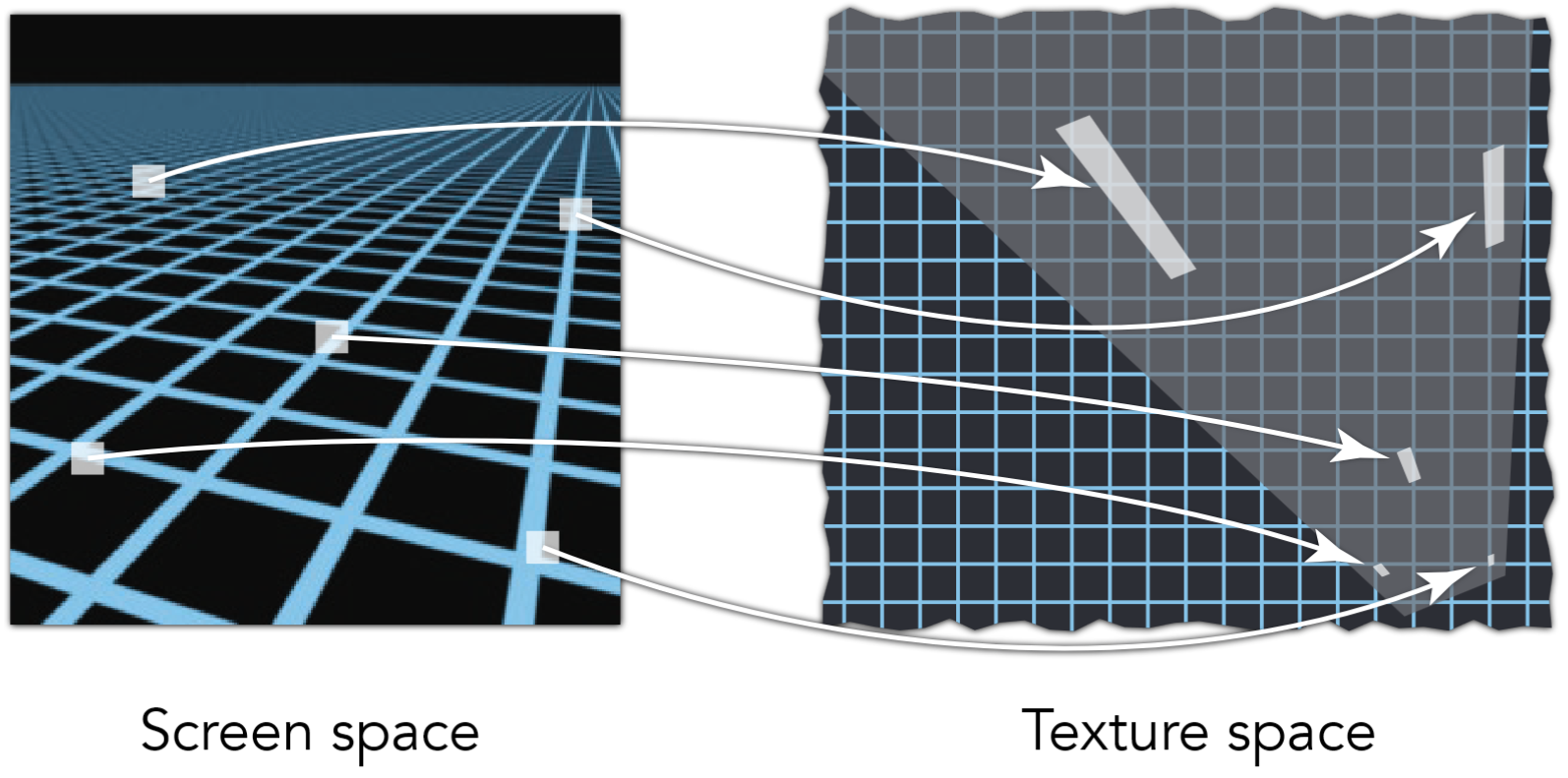
各向异性过滤
另一种方法为各向异性过滤 Anisotropic Filtering。
和 Mipmap 不同,Ripmap 使用了不同纵横比的压缩纹理,这样允许对正常的矩形查询,能解决一部分问题。使用了 $3$ 倍的空间。
EWA 过滤
通过将一个图形拆分成几个图形的叠加,我们可以较好地计算不规则区域的平均。
纹理应用
环境纹理
在观察一个物体时,会有来自四面八方的光照,将其颜色记录下来就是环境纹理。

如果将环境光记录在球体上,那么在展开成平面图时会在“两极”发生严重扭曲;
如果将环境光记录在立方体上,展开后的效果会好很多。
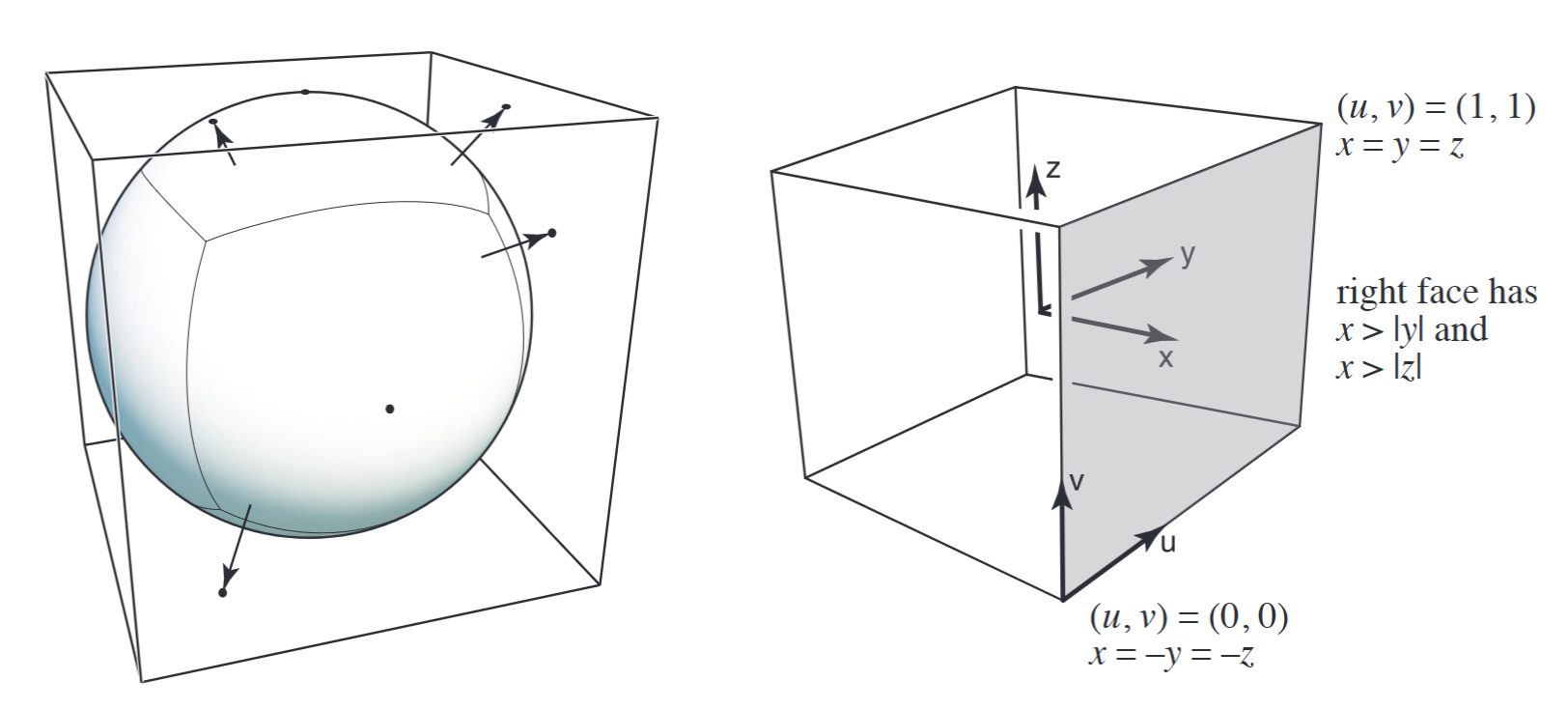

纹理高度
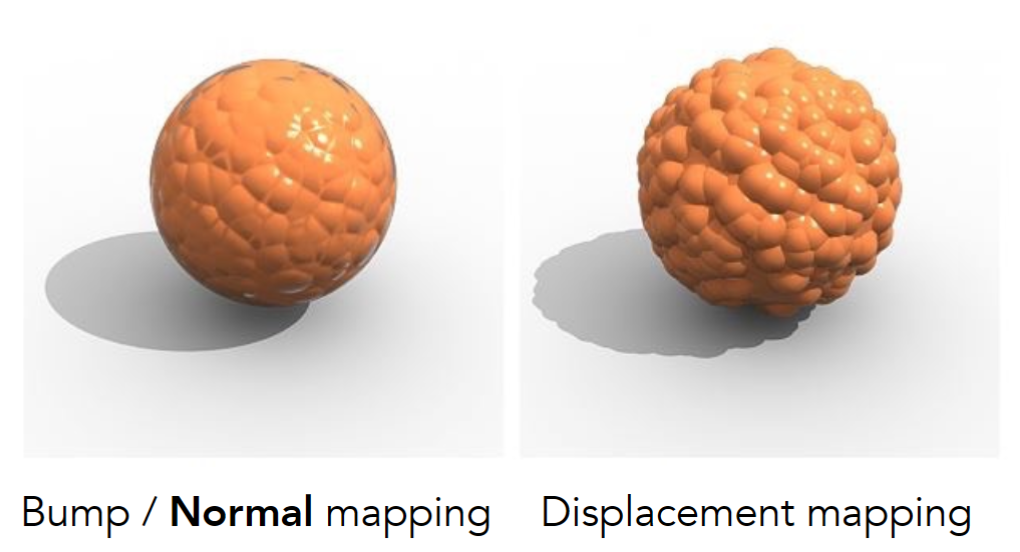
如果给纹理加上高度,那么在着色时各点的法线会发生变化,可以在不修改物体几何表示的情况下增加凹凸质感,在视觉上使物体的结构变复杂了。

二维情况
假设原来的法线为 $\vec n(p) = (0, 1)$。那么在引入高度 $h(p)$ 之后,有切线 $\mathrm{d}h = c(h(p + 1) - h(p))$,新的法线变成 $\vec n(p) = (-\mathrm{d}h, 1)$,其中 $c$ 反应纹理对法线的实际影响。
三维情况
假设原来的法线为 $\vec n(p) = (0, 0, 1)$。类比求偏导的方法,有
$$
\frac{\mathrm{d}h}{\mathrm{d}u} = c_1 (h(p + \vec u) - h(p))
$$ $$
\frac{\mathrm{d}h}{\mathrm{d}v} = c_2 (h(p + \vec v) - h(p))
$$
其中 $\vec u, \vec v$ 为对应方向的单位向量,$c_1, c_2$ 反应纹理对法线的实际影响。
$(1, 0, \dfrac{\mathrm{d}h}{\mathrm{d}u})$ 与 $(0, 1, \dfrac{\mathrm{d}h}{\mathrm{d}v})$ 叉乘得到新法线, $\vec n(p) = (- \dfrac{\mathrm{d}h}{\mathrm{d}u}, - \dfrac{\mathrm{d}h}{\mathrm{d}v}, 1)$。
位移贴图
位移贴图和高度类似,但是实际上真移动了三角形的顶点。这就要求三角形足够小足够多,才能满足纹理所定义的变化。
在现有技术中,DirectX 不要求初始的模型足够精细,而在应用位移贴图的过程中检测三角形是否足够小,如果不够进行动态拆分(动态曲面细分 dynamic tessellation)后再应用。
三维纹理
三维纹理使得物体的每一个点都有对应属性。实际上并不直接定 义每个点的值,而是定义一组噪声函数,在需要一个点的属性时计算它的值。噪声函数还可以应用在地图生成等领域。
在医学领域,核磁共振成像、CT成像等可以返回三维空间的信息,在三维空间中渲染出结果,也可以认为是三维的纹理。